here's a tutorial on that subject.
http://onlinestatbook.com/2/normal_distribution/normal_approx.html
here's another one.
http://www.regentsprep.org/regents/math/algtrig/ats7/blesson3.htm
the trick is to keep looking at online tutorials until you find one that you can actually understand.
i did a search for "normal distribution approximation of the binomial" and the above two are ones that i found the easiest to understand.
let's do the binomial first.
the binomial formula is:
p(x) = c(n,x) * p^x * q^(n-x)
x is the number of occurrences you are looking for out of n possible occurrences.
p is the probability of success.
q is the probability of failure which is equal to 1 - p.
for your problem:
n = 25
p = .5
q = .5
x is from 15 to 18.
you need 4 calculations for x = 15 to 18 and then you need to add them up to get the total probability.
p(15) = c(25,15) * .5^15 * .5^10 = .0974166393
p(16) = c(25,16) * .5^16 * .5^9 = .0608853996
p(17) = c(25,17) * .5^17 * .5^8 = .0322334468
p(18) = c(25,18) * .5^18 * .5^7 = .0143259764
add them up and you get a probability of .2048614621.
the normal approximation to this binomial would be calculated as follows:
n = 25
p = .5
q = .5
m = n * p = .5 * 25 = 12.5
that's the mean of the normal distribution.
s = sqrt (n * p * q) = sqrt (25 * .5 * .5) = sqrt (6.25) = 2.5
that's the standard deviation of the normal distribution.
you need to find the z-score of the lower bound and the z-score of the upper bound.
you need to correct for the fact that the normal distribution is a continuous distribution while the binomial distribution is a discrete distribution.
you do this by subtracting .5 from the lower bound and adding .5 to the upper bound of the normal distribution.
15 to 18 becomes 14.5 to 18.5.
you need to find the z-score of the lower bound and the z-score of the upper bound.
the formula for z-score is:
z = (x-m) / s
x is the z-score.
x is the actual score.
m is the mean of the normal distribution.
s is the standard deviation of the normal distribution.
your lower z-score will be z = (14.5 - 12.5) / 2.5.
that makes the lower z-score equal to .8
your upper z-score will be z = (18.5 - 12.5) / 2.5.
that makes the upper z-score equal to 2.4.
you now look in the z-score table to find the probability of getting a z-score between .8 and 2.5.
that probability (using my ti-84 plus calculator) is equal to .2036578048.
the binomial distribution result was .2048614621.
the normal approximation of the binomial result was .2036578048.
that's not bad.
the larger the number of possible occurrences, the closer the approximation becomes.
i used some online calculators to make sure i did it correctly.
the online binomial calculator i used gave the following result.
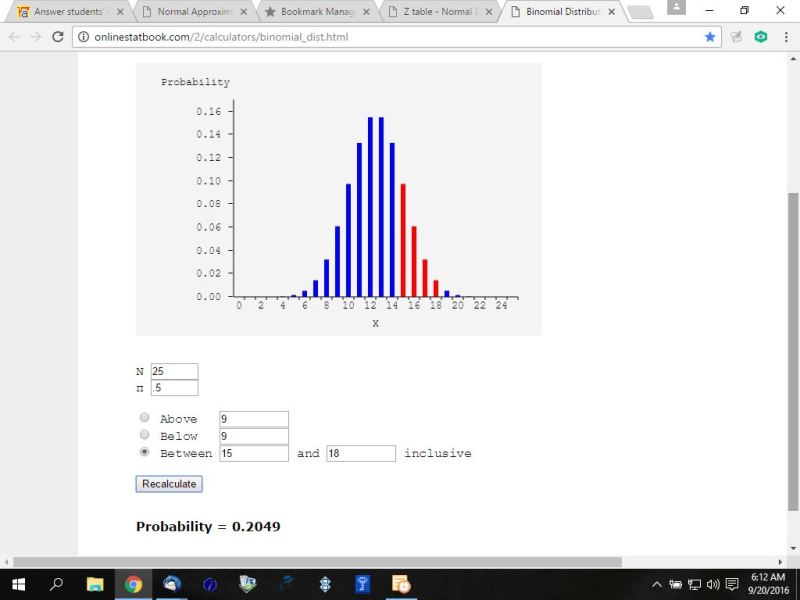
the online normal distribution calculator i used gave the following result.

these confirmed that i did the calculations correctly.