Question 1029561: Could you please help me with this question?
Calís Coffee prints prize coupons under the rims of 20% of its paper cups. If you buy ten cups of coffee.
What is the probability that you would win at least seven prizes?
What is your expected number of prizes?
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Question:
Could you please help me with this question?
Calís Coffee prints prize coupons under the rims of 20% of its paper cups. If you buy ten cups of coffee.
(a) What is the probability that you would win at least seven prizes?
(b) What is your expected number of prizes?
Solution:
Here the probability of winning is constant at 20%, and assuming the ten cups of coffee are purchased at random and independently, then we can apply the binomial distribution, given by:
P(x,n,p)=
where C(n,x) is the number of combinations of x objects taken out of n,
p=probability of success
n=number of objects in the sample.
(a) probability of winning at least 7 prizes
P(7≤x≤10,10,0.2)
=P(7,0,0.2)+P(8,0,0.2)+P(9,0,0.2)+P(10,0,0.2)
=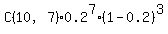 + +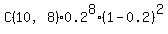 + +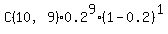 + +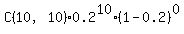
=0.00078643+0.00007373+0.00000410+0.00000010
=0.0008644 (to 7 figures)
(b) expected value in a binomial distribution is np, which means the expected number of prizes is n*p=10*0.2=2 prizes.
You can read about binomial distributions and more examples at:
http://www.euclid.host-ed.me/probability/binomialDistribution.html
|
|
|