SOLUTION: A dish contains n strands of cooked spaghetti. Two ends are chosen at random and tied together. Two other ends are selected and tied together.If this process continues until there

Choose one particular strand to begin with, call it strand A.
Think of it being bent in an arc like this: 
Think of the loop being created beginning with strand A and tieing on 
strands one by one forming a single loop clockwise.

Choose one of the remaining n-1 strands as the 2nd strand to 
tie onto the right end of the 1st strand (strand A) in n-1 ways.
Choose which end of that strand to tie onto the right end
of the 1st strand in 2 ways.

Choose one of the remaining n-2 strands as the 3rd strand to tie 
onto the end of the 2nd strand in n-2 ways.
Choose which end of the 3rd strand to tie onto the untied end
of the 2nd strand in 2 ways.

Choose one of the remaining n-3 strands as the 4th strand to tie 
onto the untied end of the 3rd strand in n-3 ways.
Choose which end of the 4th strand to tie onto the untied end 
of the 3rd strand in 2 ways. 

...

Choose one of the remaining 2 strands as the (n-1)st strand to tie 
onto the right end of the (n-2)nd strand in 2 ways.
Choose which end of the (n-1)st strand to tie onto the untied end 
of the (n-2)nd strand in 2 ways.

Choose the 1 remaining strand as the nth strand to tie 
onto the untied end of the (n-1)st strand in only 1 way.
Choose which end of the nth strand to tie onto the untied end 
of the (n-1)st strand in 2 ways.

Finally tie the untied end of the nth strand onto the left end
of strand A.

So the number of ways that can be done is 

(n-1)*2*(n-2)*2*(n-3)*2*...*2*2*1*2 = (n-1)!*2^(n-1)

This is independent of the particular strand that was chosen
for strand A.

So the numerator of the desired probability is (n-1)!*2^(n-1)
 

Next we must find the denominator of the probability.
This is the hard part.

First we find the number of ways he could tie them in a certain
order, and then we will "unorder" them by dividing by n!.

There are 2n ends.

We pick the 1st pair of ends to tie together in 
C(2n,2) = 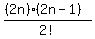 ways.
We pick the 2nd pair of ends to tie together in 
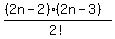C((2n-2),2) =  ways.
We pick the 3rd pair of ends to tie together in 
C((2n-4),2) = .

...
We pick the (n-1)st pair of ends to tie together in 
C(4,2) = .
We pick the nth pair of ends to tie together in 
C(2,2) = .

So the number of orderings of tieings is:


 
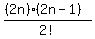
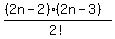
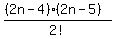
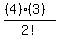
That is equal to 



However, any given result of tied ends could have resulted from 
any of n! sequences of tieings.

Therefore we must divide   by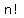 

So the denominator of the desired probability is

   

-----

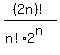So the desired probability of (a) is 



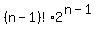
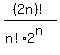
Invert and multiply and that can be simplified to 



If we multiply top and bottom by n, we get

That's just 1 way out of the denominator calculated above, or

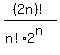, or



Edwin