Question 414107: Why is it impossible to factor out the sum of two squares? I know how to factor the difference but I was just curious. Thanks!
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! Say you have two variables, x and y. Now I'm going to further say that x and y have nothing in common (except 1, but we're going to ignore that). So we can't factor the GCF out of  because it would be trivial.
Now square each term to get  . Let's assume that we can factor this.
So using the AC method, we can think of as  and we can clearly see that the 3 coefficients are 1,0, and 1
Multiply the first and last coefficient to get 1*1 = 1.
Now the big question is: what two numbers BOTH multiply to 1 (the product above) AND add to 0?
Any ideas?
.....
If you're stumped, you have a very good reason as there are no two numbers that fit both conditions. Notice how the two numbers multiply to a positive result. So the two numbers are
a) both positive, or
b) both negative
But if you add two positive numbers (no matter how small), you will NOT get zero. Likewise, adding two negative numbers will NEVER give you zero. In order for  to be true (where  and 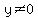 ) x and y MUST have different signs. It's not possible otherwise.
So this shows us that no two numbers both multiply to 1 and add to 0
This consequently means that cannot be factored.
If you need more help, email me at jim_thompson5910@hotmail.com
Also, please consider visiting my website: http://www.freewebs.com/jimthompson5910/home.html and making a donation. Thank you
Jim
|
|
|
