i used the TI-BA-II financial calculator.
the BA stands for Business Analyst.
my entries are:
pv = 0
fv = 50,000 (entered without the comma)
r = .0048073071%
n = 15
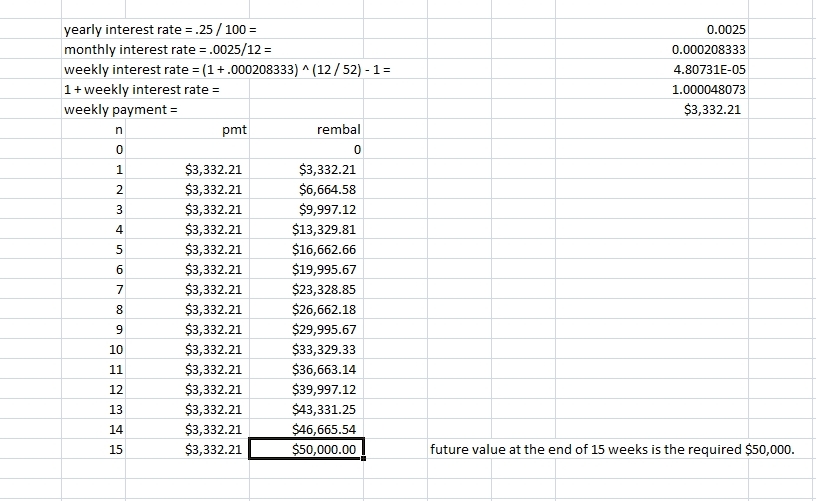
the calculator tells me that the weekly payments need to be 3332.211772.
the total payments = 15 * that = 49,983.17658.
the rest is interest earned from the weekly payments of 3332.211772.
i used excel to show the remaining weekly balance.
it is shown below.
i also used an online calculator at https://arachnoid.com/finance/index.html to show you what the inputs would look like and what the output would look like if you used this online calculator.
the inputs to this calculator are shown below:

the output from this calculator is shown below:

one answer to your question.
the principal is the amount that is invested.
in your problem, that would be the $3,332.21 that is invested at the end of each week for 15 weeks.
the future value is the principal plus interest earned during the 15 week investment period.
your total investment was 15 * 3,332.21 = $49,983.15
the difference between that and the future value was the interest, which equaled $16.85.
the calculation of the weekly interest rate was critical to the success of this procedure.
the yearly interest rate percent was divided by 12 to get the monthly interest rate percent.
this was divided by 100 to get the monthly interest rate.
1 was added to this and the result was then raised to the 12/52 power to get the weekly interest rate plus 1.
1 was subtracted from this to get the weekly interest rate.
this was multiplied by 100 to get the weekly interest rate percent.
the weekly interest rate percent is what was entered as the rate in the calculator.
this was calculated to be ((1 + .25/1200) ^ (12/52) - 1) * 100 = .0048073071.
note that .25/1200 is equal to .25 / 12 to get the monthly interest rate percent which is divided by 100 to get the monthly interest rate.
note that when you raise that to the (12/52) power, you are raising it to the 12th power to get the effect yearly interest rate + 1, and then you are taking the 52d root of that to get the weekly interest rate + 1.
the procedure to find the weekly interest rate percent is shown below.
.25% is the yearly interest rate percent which is also known as the apr (annual percentage rate).
.25% / 100 = .0025 is the yearly interest rate.
this is divided by 12 to get the monthly rate.
.0025 / 12 = .0002083333333 = the monthly interest rate.
add 1 to this to get 1.00020833333.
raise that to the 12th power to get the effective yearly interest rate plus 1.
subtract 1 from that to get the effective yearly interest rate.
multiply that by 100 to get the effective yearly interest rate percent.
effective yearly interest rate + 1 = (1.00020833333) ^ 12 = 1.002502867
1.002502867 - 1 = .002502867 = the effective yearly interest rate.
.002502867 * 100 = .2502867 = the effective yearly interest rate percent.
take the 52d root of the effective yearly interest rate + 1 to get the weekly interest rate + 1.
that is equal to (1.002502867) ^ (1/52) = 1.000048073.
subtract 1 from that to get the weekly interest rate.
that is equal to .000048073071
multiply that by 100 to get the weekly interest rate percent.
that is equal to .0048073071.
that is what was entered into the calculator as the weekly interest rate percent.
the number of time periods in the calculator was set to 15 because you were investing at the end of each week for 15 weeks.
the last input is telling you that the investment is made at the end of each week.
that's the switch where you select beginning or end.
the only nominal interest rate was the yearly interest rate.
that was divided by 12 to get the monthly interest rate.
the monthly interest rate and the weekly interest rate were both effective interest rates.
this is a lot to understand.
if you need to ask any further questions about it, send me an email and i'll answer as best i can.
your solution is that she has to deposit $3,332.21 at the end of each week for 15 weeks so that she will have $50,000 for her year end party.