SOLUTION: Find the polynomial function with the given zeros: 3, 3i, 3+3i. Please show all work, thank you!

First we find a polynomial equation with solutions

3, 3i, 3+3i

Since 3+3i is a zero, so is its conjugate 3-3i

Since 3i is an imaginary zero, so is its conjugate. To find the 
conjugate of 3i, write it as 0+3i and so its conjugate is 0-3i
which is just -3i.

So all the zeros are 3, 3i, -3i, 3+3i. 3-3i

Set x = to each of those:

   x=3;    x=3i;      x=-3i;    x=3+3i;      x=3-3i

Get 0 on the right side of each of those:

 x-3=0;  x-3i=0;     x+3i=0;  x-3+3i=0; x-3+3i=0

Multiply all the left sides together, putting each
in parentheses, ant them equl to all the right sides
multiplied together.  Since the right sides are all 0, 
multiplying them all together gives 0. So we have:

  (x-3)(x-3i)(x+3i)(x-3+3i)(x-3+3i) = 0

That's a lot of multiplying, but when you have collected
all the terms, and taken care of all the powers of i, you 
will have:

  

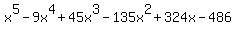So the polynomial function that has those given zeros is

  .

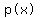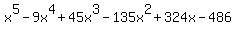Edwin