Question 1183719: Given regular hexagon ABCDEF, with center O and sides of length a. Let G be the midpoint of BC. Let H be the midpoint of DE. AH intersects EB at J and FG intersect EB at K. Find JK. (Hint: Draw auxiliary lines HG and DA.
Found 2 solutions by greenestamps, robertb:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I haven't come up with a standard geometric solution; but a solution using coordinate geometry works nicely.
Let the origin (0,0) be the center of the regular hexagon; and for simplicity choose a "nice" number for the side length -- I chose 12. My hexagon then has vertices
A(-12,0)
B(-6,6sqrt(3))
C(6,6sqrt(3))
D(12,0)
E(6,-6sqrt(3))
F(-6,6sqrt(3))
From those, we get
G(0,6sqrt(3)) [midpoint of BC]
H(9,-3sqrt(3)) [midpoint of DE]

Find the equations of lines AH, BE, and FG
BE: y=(-sqrt(3))x
FG: y=(2sqrt(3))x+6sqrt(3)
AH: slope = (-3sqrt(3)/21) = -sqrt(3)/7
equation: y=(-sqrt(3)/7)(x+12) = (-sqrt(3)/7)x-12sqrt(3)/7
Find the coordinates of K, the intersection of FG and EB
(-sqrt(3)x)=2sqrt(3)x+6sqrt(3)
-3sqrt(3)x=6sqrt(3)
x=-2
y=-sqrt(3)x = 2sqrt(3)
Find the coordinates of J, the intersection of AH and BE
(-sqrt(3)x)=(-sqrt(3)/7)x-12sqrt(3)/7
(-7sqrt(3)x=-sqrt(3)x-12sqrt(3)
-6sqrt(3)x=-12sqrt(3)
x=2
y=-sqrt(3)x=-2sqrt(3)
So J is (2,-2sqrt(3)) and K is (-2,2sqrt(3))
The length of JK is then given by the distance formula
(JK)=sqrt(4^2+(4sqrt(3))^2) = sqrt(16+48) = sqrt(64) = 8
ANSWER: JK = 8
Or, since I used a=12,
ANSWER: JK = (2/3)a
Note the symmetry of the two points J and K with respect to the center of the hexagon suggests that a standard geometric solution to the problem should be possible; but I haven't yet seen it.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider hexagon ABCDEF with the vertices labeled clockwise. From the hint, line GH would be parallel to both lines CD and AF.
The distance between lines CD and AF is 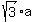 . (Why is this so?) . (Why is this so?)
Incidentally, since line GH is three-fourth of this distance away from line AF, the distance between lines GH and AF is  . .
Let P be the intersection of lines FG and AH.
Let Q be the midpoint of line AF, and let R be the midpoint of line GH.
Then the points P, Q, R, and the center O are all collinear.
===> Triangle GRP is similar to triangle FQP.
We know that  and and  . Now let . Now let  , so that , so that  . .
By similarity of triangles,
 , i.e., , i.e.,

===>  after solving for after solving for  . .
This implies that segment PO has length  . .
Also,  . .
If we let K be the intersection of lines BE and FG, the triangle KOP will be similar to triangle GRP. Then

===>  . .
But  is half of is half of  . Therefore, . Therefore,
 . .
|
|
|