|
Question 1125455: If the equation of line l is ax + by = c, find its slope, x- and y-intercepts, and the line through the origin perpendicular to l.
Found 2 solutions by josmiceli, Theo:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the equation of the line is ax + by = c
you want the slope, the x and y intercepts, and the line through the origin perpendicular to the line.
convert the equation of the line from standard form (ax + by = c) to slope intercept form (y = mx + b)
start with ax + by = c
subtract ax from both sides of the equation to get by = -ax + c.
divide both sides of the equation by b to get y = -a/b * x + c/b.
the slope is -a/b.
the y-intercept is c/b.
the x-intercept is found by setting y equal to 0 and solving for x.
start with y = -a/b * x + c/b.
replace y with 0 to get 0 = -a/b * x + c/b.
subtract c/b from both sides of the equation to get -c/b = -a/b * x.
multiply both sides of this equation by b/-a to get -c/b * b/-a = x.
simplify to get c/a = x.
the slope is -a/b
the y-intercept is c/b
the x-intercept is c/a
if a line is perpendicular to the another line, then the slope of the line perpendicular to the other line is a negative reciprocal of the slope of the other line.
since the slope of the line is -b/a, then the slope of the line perpendicular to it will be a/b.
you now have:
the slope is -a/b
the y-intercept is c/b
the x-intercept is c/a
slope of the line perpendicular to this line is b/a.
since that line goes through the origin, then y-intercept is 0 and the equation of the line is y = b/a.
you now have:
the slope is -a/b
the y-intercept is c/b
the x-intercept is c/a
slope of the line perpendicular to this line is b/a.
equation of the line perpendicular to this line is y = b/a * x.
to confirm that this is correct, we will take a line and subject it to the requirements of this to see if they are accurate.
the line i chose is 10x + 5y = 20
the standard form is ax + by = c which makes:
a = 10
b = 5
c = 20
using what we found generically, then:
the slope is -a/b which becomes -10/5 = -2.
the y-intercept is c/b which becomes 20/5 = 4
the x-intercept is c/a which becomes 20/10 = 2
slope of the line perpendicular to this line is b/a which becomes 5/10 = .5
since that line goes through the origin, then y-intercept is 0 and the equation of the line is y = b/a * x which becomes y = .5x
i graphed the line and the line perpendicular to it to see if the generic form predicts the particular form i chose for an example.
the graph is shown below:
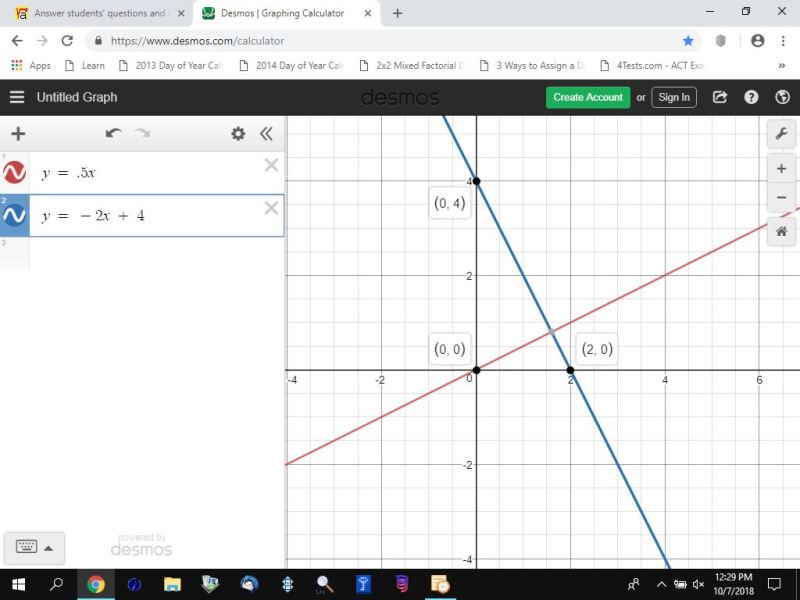
the line is in blue.
the line perpendicular to it is in red.
the x-intercept is 2 as it was predicted to be.
the y-intercept is 4 as it was predicted to be.
the line perpendicular to it goes through the origin as it was predicted to be.
the particular form was predicted by the general form, so the general form is assumed to be good.
|
|
|
| |