|
Question 1205030: Given 30-60-90 triangle with sides p\sqrt(6) , p\sqrt(2 ), q\sqrt(3); find p, q
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Don't use "\" -- it might have a special meaning in some area(s) of mathematics.
I assume the side lengths are p/sqrt(6), q/sqrt(3), and p/sqrt(2).
The squares of the side lengths are then p^2/6, q^2/3, and p^2/2.
On first glance, with the denominators 6, 3, and 2, I immediately see that, if p and q are both equal to the same number x, then I have x^2/6+x^2/3=x^2/2, which is true for all values of x.
So the problem has an infinite number of solutions in which p=q.
But there might be other solutions hiding somewhere, so lets' look at the problem more closely.
We know that p/sqrt(2) is greater than p/sqrt(6); but q/sqrt(3) could be less than or greater than p/sqrt(2). So there are two cases to consider: the longest side (hypotenuse) can be either p/sqrt(2) or q/sqrt(3).
Case 1: the hypotenuse is p/sqrt(2)
(Note this is the case discussed informally above.)






Case 2: The hypotenuse is q/sqrt(3)






This case also has an infinite number of solutions, where p is any number x and q is x*sqrt(2).
ANSWER:
p = any number;
q = p OR q=p*sqrt(2)
Answer by ikleyn(52864)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given 30-60-90 triangle with sides p/sqrt(6) , p/sqrt(2 ), q/sqrt(3); find p, q
~~~~~~~~~~~~~~~~~~~~~
Notice that I rewrote the condition using normal designations for the division operation.
Two sides 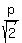 and and 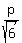 have the ratio have the ratio
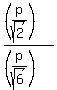 = = 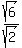 = =  .
In combination with the given fact that the triangle is 30-60-90,
it means that .
In combination with the given fact that the triangle is 30-60-90,
it means that 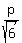 is the shorter leg, while is the shorter leg, while 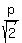 is the longer leg.
+-----------------------------------------------+
| It admits only one interpretation, |
| and no other interpretation is admittable. |
+-----------------------------------------------+
Hence, is the longer leg.
+-----------------------------------------------+
| It admits only one interpretation, |
| and no other interpretation is admittable. |
+-----------------------------------------------+
Hence, 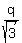 is the hypotenuse, and we can write is the hypotenuse, and we can write
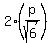 = = 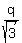 (the hypotenuse length is twice the shorter leg), since the triangle is 30-60-90.
It gives q =
(the hypotenuse length is twice the shorter leg), since the triangle is 30-60-90.
It gives q = 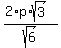 = = 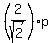 = = 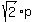 .
So, the sides are: .
So, the sides are: 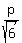 is the shorter leg, is the shorter leg, 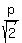 is the longer leg and is the longer leg and 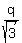 = = 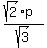 is the hypotenuse.
We can write then Pythagorean equation is the hypotenuse.
We can write then Pythagorean equation
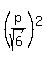 + + 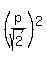 = = 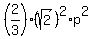 ,
or ,
or
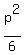 + + 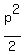 = = 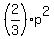 , ,
 + +  = =  , ,
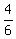 = =  , ,
 = =  ,
which is an identity.
At this point, the problem is solved in full.
ANSWER. p can be any real positive number; then q = ,
which is an identity.
At this point, the problem is solved in full.
ANSWER. p can be any real positive number; then q = 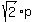 . There are infinitely many solutions. . There are infinitely many solutions.
Solved.
|
|
|
| |