SOLUTION: Triangle $ABC$ has vertices $A(2, 3),$ $B(1, -8)$ and $C(-3, 2).$ The line containing the altitude through $A$ intersects the point $(0, y).$ What is the value of $y$?

Algebra ->  Percentage-and-ratio-word-problems -> SOLUTION: Triangle $ABC$ has vertices $A(2, 3),$ $B(1, -8)$ and $C(-3, 2).$ The line containing the altitude through $A$ intersects the point $(0, y).$ What is the value of $y$?      Log On


   

Question 1203459: Triangle $ABC$ has vertices $A(2, 3),$ $B(1, -8)$ and $C(-3, 2).$ The line containing the altitude through $A$ intersects the point $(0, y).$ What is the value of $y$?
Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
Triangle ABC has vertices A(2, 3), B(1, -8) and C(-3, 2).
The line containing the altitude is perpendicular to the line containing B(1, -8) and C(-3, 2)
find a slope of that line:
m=%282-%28-8%29%29%2F%28-3-1%29=%282%2B8%29%2F-4=10%2F-4=-5%2F2
The line containing the altitude is perpendicular, so slope will be m=-1%2F%28-5%2F2%29=2%2F5
then, using point slope formula , the line containing the altitude will be
y-y1=m%28x-x1%29
the point A(2, 3) and m=2%2F5
y-3=%282%2F5%29%28x-2%29
y-3=%282%2F5%29x-2%282%2F5%29
y=%282%2F5%29x-4%2F5%2B3
y=%282%2F5%29x-4%2F5%2B3
y=%282%2F5%29x%2B11%2F5
y=%282%2F5%29x%2B2.2
then
the point P(0, y) will be
y=%282%2F5%290%2B11%2F5=11%2F5
the point (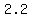0, 2.2)



Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Answer: y = 11/5 = 2.2


Explanation

Compute the slope of line BC


m+=+%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29

m+=+%282+-+%28-8%29%29%2F%28-3+-+1%29

m+=+%282+%2B+8%29%2F%28-3+-+1%29

m+=+%2810%29%2F%28-4%29

m+=+-5%2F2
The slope of -5/2 means "go down 5 units every time we go 2 units to the right".
In short: "down 5, right 2".

The negative reciprocal slope will have us do two things:
flip the fraction
flip the sign

-5/2 becomes 2/5

The altitude line through point A has a slope of 2/5
Apply point-slope form
y+-+y%5B1%5D+=+m%28x+-+x%5B1%5D%29

y+-+y%5B1%5D+=+%282%2F5%29%28x+-+x%5B1%5D%29 Plug in perpendicular slope

y+-+3+=+%282%2F5%29%28x+-+2%29 Plug in coordinates of point A

y+-+3+=+%282%2F5%29x+%2B+%282%2F5%29%28-2%29

y+-+3+=+%282%2F5%29x+-+4%2F5

y+=+%282%2F5%29x+-+4%2F5+%2B+3

y+=+%282%2F5%29x+-+4%2F5+%2B+3%2A%285%2F5%29

y+=+%282%2F5%29x+-+4%2F5+%2B+15%2F5

y+=+%282%2F5%29x+%2B+%28-4+%2B+15%29%2F5

y+=+%282%2F5%29x+%2B+11%2F5
This is the equation of the altitude through point A. It is perpendicular to side BC.

Plug in x = 0 to find that y = 11/5 = 2.2 which is the final answer.

Here's the diagram

The blue line is the altitude through point A.
It intersects the y axis at (0, 11/5) = (0,2.2) which is marked as point D.