SOLUTION: I am trying to figure out how the area of a right trapezoid and the shorter base was calculated. From a diagram, the longer base is 8cm. The shorter base is unknown. The height is

Algebra.Com
Question 1136847: I am trying to figure out how the area of a right trapezoid and the shorter base was calculated. From a diagram, the longer base is 8cm. The shorter base is unknown. The height is 3 cm. The slant height is 5 cm. I do not know how the total area was calculated at 18cm (squared) and the shorter base was calculated at 4 cm.
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52818)   (Show Source): You can put this solution on YOUR website!
.
1.  Make a sketch.



2.  Your trapezoid has ONLY ONE obtuse angle.

    From the vertex of this obtuse angle draw the height (the perpendicular) to the longer base.



3.  You will obtain a right angled triangle.

    Do you see it ?


    Its hypotenuse is 5 cm.
    Its leg is 3 cm.

    Hence, its other leg is 4 cm (3-4-5 right angled triangle).



4.  Hence, the shorter base of the trapezoid is 8 - 4 = 4 centimeters.

    Is it clear so far ?



5.  To find the area of the trapezoid, use the basic formula


    Area of the trapezoid =  =  = 18 square centimeters.


Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
the longer base is equal to 8 cm.
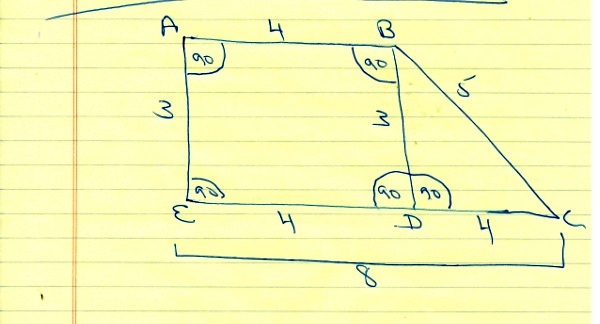
the height is equal to 3 cm.
the slant height is equal to 5 cm.

if it is a right trapezoid, then two of the angles have to be right angles.

label your trapezoid ABCDE clockwise from top left.

angle A and angle E are right angles.

the slant height is side BC = 5.

the height is BD = 3 and AE = 3.

the triangle on the right is right triangle BCD where the 90 degree angle is BDC.

angles BDE and ABD are also right angles.

use pythagorus to find the length of DC, which is 4.

pythagorus says 3^2 + x^2 = 5^2

solve for x to get x = sqrt(5^2 - 3^2) = sqrt(16) = 4.

that makes ED = 4 and, consequently AB = 4 because ABDE forms a rectangle.

the area of the trapezoid is equal to the area of the rectangle plus the area of the triangle.

this becomes 4 * 3 + 1/2 * 3 * 4 which becomes 12 + 6 = 18.

here's my diagram.

$$$
RELATED QUESTIONS

Timmy was asked to find the area of an isosceles trapezoid. This trapezoid had a shorter... (answered by ikleyn)
a trapezoid with area 152 has a longer base of length 22. The shorter base and the height (answered by Boreal)
A trapezoid has a shorter base length of 14, an acute base angle of 72°, and a height of (answered by Edwin McCravy)
I am having problems trying to figure this problem out. Find the exact area of a... (answered by edjones,josmiceli,mananth)
please illustrate the figure..the longer base of an isosceles trapezoid is 40, one leg is (answered by venugopalramana)
How do I set up this proof, figure out a diagram, and givens?: The line drawn from the... (answered by mbotros)
Help to solve and figure out Rose's garden is in the shape of a trapezoid. If the height... (answered by checkley71)
How to find the area of a trapezoid if the top part was 8 the height was 6 and the base... (answered by solver91311)
The longer diagonal of a right trapezoid is 13 cm. The longer base is 12 cm. Find the... (answered by ikleyn,MathTherapy)