Thus the determinant is defined for any square matrix with 3 rows and 3 columns.
Sometimes the determinant of a matrix
|

|
is denoted as det
|
 or or
|
 . .
|
The patterns for calculation the determinant terms are shown in Figure 1a and 1b.
Each term of a determinant, additive or subtrahend, is the product of elements that
are located in different rows and different columns of a matrix.
No one single term of a determinant contains two elements from the same row. No one
single term of a determinant contains two elements from the same column.
|

Fig. 1a. (+)-Patterns
for the determinant
|

Fig. 1b. (-)-Patterns
for the determinant
|
Examples. Calculate determinants of matrices
 , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  , ,  . .
Lesson HOW TO solve system of linear equations in three unknowns using determinant (Cramer's rule)
If

is a system of three linear equations in three unknown  , ,  and and  , where , where  , ,  , ,  , ,  , ,  , ,  , ,  , ,  and and  are coefficients and are coefficients and  , ,  and and  are right side are right side
constants, then the solution of this system is (the Cramer's rule)
 , ,  , ,  . .
Here the matrix  in the denominators is the coefficient matrix of the system formed by its coefficients. It is assumed that the coefficient matrix in the denominators is the coefficient matrix of the system formed by its coefficients. It is assumed that the coefficient matrix
has a non-zero determinant. This is the necessary condition for the Cramer's rule applicability.
The matrix in the numerator for the first unknown  is obtained from the coefficient matrix after replacing its first column by the right sides vector is obtained from the coefficient matrix after replacing its first column by the right sides vector  . .
The matrix in the numerator for the second unknown  is obtained from the coefficient matrix after replacing its second column by the right sides vector is obtained from the coefficient matrix after replacing its second column by the right sides vector  . .
The matrix in the numerator for the third unknown  is obtained from the coefficient matrix after replacing its third column by the right sides vector is obtained from the coefficient matrix after replacing its third column by the right sides vector  . .
Examples 1 and 2. Solve theses systems of three linear equations in three unknowns
 
Lesson Solving systems of linear equations in three unknowns using determinant (Cramer's rule)
Problems 1, 2 and 3. Solve these systems of three linear equations in three unknowns
  
Problem 4. Solve the system of three non-linear equations in three unknowns

Lesson Solving word problems by reducing to systems of linear equations in three unknowns
Problem 1. A concert audience of 400 people consists of adults, students, and children. The ticket prices are $40 for adults, $20 for students, and $10 for
children. The total amount of money taken in is $10600. The number of children tickets sold is in 200 less than the number of adult and student tickets
in total. How many adults, students, and children are in attendance?
Problem 2. Maria invested a total $26000 into three accounts: a saving account paying 3% interest, a CD deposit paying 4% interest, and a bond paying 5% interest.
Her total annual interest from the three investments was $1000. The interest from the saving account was $460 less than the total interest from the other
two investments. How much did she invest at each rate?
Problem 3. Ron attends a cocktail party (with his graphing calculator in his pocket). He wants to limit his food intake to
109 g protein, 103 g fat, and 153 g carbohydrate.
According to the health conscious hostess, the marinated mushroom caps have 3 g protein, 5 g fat, and 9 g carbohydrate;
the spicy meatballs have 14 g protein, 7 g fat, and 15 g carbohydrate;
and the deviled eggs have 13 g protein, 15 g fat, and 6 g carbohydrate.
How many of each snack can he eat to obtain his goal ?
Problem 4. There were 240 persons in a picnic. There were 20 more men than women and 20 more adults than children.
How many men were there in the picnic ?
Lesson The tricks to solve some word problems with three and more unknowns using mental math
Problem 1. Alan, Bob and Cleve weight together 255 pounds. Bob, Cleve and Dan weight together 267 pounds.
Cleve, Dan and Alan weight together 262 pounds. Dan, Alan and Bob weight together 257 pounds.
What is the weight of each of the boys?
Problem 2. Jonny has a collection of coins in nickels (5 cents), dimes (10 cents) and the quarters (25 cents).
The amount of money in nickels and dimes in the collection is of 130 cents.
The amount of money in nickels and quarters is of 285 cents. The amount of money in dimes and quarters is of 295 cents.
How many coins of each nomination are there in the collection?
Problem 3. Alice and Barbara weight together in 50 pounds more than Christi weights.
Alice and Christi weight together in 52 pounds more than Barbara weights.
Barbara and Christi weight together in 54 pounds more than Alice weights.
Find the weight of each of the girls.
Problem 4. Five baskets contain coconuts. The first and second baskets together have a total of 52 coconuts.
The second and third baskets have 43 coconuts. The third and fourth baskets have 34 coconuts.
The fourth and fifth baskets have 30 coconuts, and the first and fifth baskets have 47 coconuts.
How many coconuts are in each basket?
Problem 5. In a triangle, the sum of the measures of its first and the second side is in 2 cm greater than the measure of the third side.
The sum of the measures of its first and the third side is in 4 cm greater than the measure of the second side.
The sum of the measures of its second and the third side is in 6 cm greater than the measure of the first side.
Find the perimeter and the measure of each side of the triangle.
Problem 6. In a quadrilateral, the sum of the measures of its first, the second and the third side is 12 cm.
The sum of the measures of its first, the third side and the fourth side is 14 cm.
The sum of the measures of its first, the third and the fourth side is 16 cm.
The sum of the measures of its second, the third and the fourth side is 18 cm.
Find the perimeter and the measure of each side of the quadrilateral.
Lesson Solving systems of non-linear equations in three unknowns using Cramer's rule
Problems 1, 2 and 3. Solve these systems of three non-linear equations in three unknowns
  
Sometime two equations are enough to find three unknowns by an UNIQUE way
Problem 1. "Sue's Candies" has a candy stall in the market.
One candy costs 5 cents each, the second costs 20 cents each and the 3rd costs 30 cents each.
In her absence due to personal necessity an honest buyer picked a total of 20 pieces of candies
costing 5 cents, 20 cents and 30 cents in the stall and left 2 pesos for their exact cost.
How many each candy of 5 cents, 20 cents, and 30 cents the honest buyer picked?
Problem 2. A farmer wants to buy 100 animals for $100.00 (must buy at least one of them)
Horses cost $5.00 each
Cows cost $3.00 each
Chickens cost $0.50 each. How many animals the farmer should buy ?
Problem 3. A furniture company makes dining room furniture.
A buffet requires 40 hours for construction 10 hours for finishing.
A chair requires 20 hours for construction and 20 hours for finishing.
A table requires 40 hours for construction and 70 hours for finishing.
The construction department has 500 hours of labor
and the finishing department has 200 hours of labor available each week.
How many pieces of each type of furniture should be produced each week if the factory is to run at full capacity?
Two very different approaches to one word problem
Problem 1. Four friends, Aisha, Ben, Cathy, and Daniel shared lunch equally.
Aisha paid 3/5 of the total amount Ben and Cathy paid.
Cathy paid $10 more than Ben.
Daniel repaid $24.00 to Aisha and some money to Ben and Cathy.
How much did Daniel repaid to Ben and how much to Cathy?
Solving word problems in three unknowns by the backward method
Problem 1. Alice, Ben and Carl collect stamps. They exchange stamps among themselves according to the following scheme:
(1) Alice gives Ben as many stamps as Ben has and Carl as many stamps as Carl has.
(2) After that, Ben gives Alice and Carl as many stamps as each of them has,
(3) and then Carl gives Alice and Ben as many stamps as each has.
If each finally has 80 stamps, with how many stamps does Ben start?
Solving system of linear equation in 17 unknowns
Problem 1. If ( , ,  , . . . , , . . . ,  ) satisfy ) satisfy
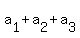 = 1, = 1,
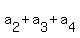 = 2, = 2,
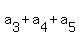 = 3,
. . . . . . . . . = 3,
. . . . . . . . .
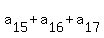 = 15, = 15,
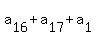 = 16, = 16,
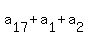 = 17, = 17,
find the value of  . .
Solving system of linear equation in 19 unknowns
Problem 1. If  , ,  , . . ., , . . .,  satisfy satisfy
 = 1, = 1,
 = 2, = 2,
 = 3,
. . . . . . . . . = 3,
. . . . . . . . .
 = 16, = 16,
 = 17, = 17,
 = 18, = 18,
 = 19, = 19,
find the value of  . .
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 2523 times.
|

