|
Question 1203997: Maria invested a total of $26000 into three accounts: a saving account paying 3\% interest, a CD deposit paying 4% interest, and a bond paying 5% interest. Her total annual interest from the three investments was $1000. The interest from the saving account was $460 less than the total interest from the other two investments. How much did she invest at each rate? (Use matrices to solve this system of linear equations.)
Found 3 solutions by ikleyn, greenestamps, math_tutor2020:
Answer by ikleyn(52884)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Maria invested a total of $26000 into three accounts:
a saving account paying 3% interest,
a CD deposit paying 4% interest,
and a bond paying 5% interest.
Her total annual interest from the three investments was $1000.
The interest from the saving account was $460 less than the total interest
from the other two investments. How much did she invest at each rate?
(Use matrices to solve this system of linear equations.)
~~~~~~~~~~~~~~~~~~~~~~
Let the unknown variables be
A = saving Account paying 3% interest;
D = CD Deposit paying 4% interest;
B = Bond paying 5% interest.
Write equations as you read the problem
A + D + B = 26000 (1)
0.03*A + 0.04*D + 0.05B = 1000 (2)
-0.03*A + 0.04*D + 0.05B = 460 (3)
Subtract equations (3) from equation (3). You will get
0.006*A = 1000 - 460 = 540 ---> A =  = 9000.
Add equations (2) and (3). You will get
0.08*D + 0.1B = 1460 (4)
Substitute A = 9000 into equation (1), You will get
D + B = 26000 - 9000,
D + B = 17000 (5)
So, now the problem is reduced from 3 unknowns to 2 unknowns
0.08*D + 0.1*B = 1460 (4)
D + B = 17000 (5)
Solve by elimination. For it, multiply equation (5) by 0.08 (both sides ).
0.08*D + 0.1* B = 1460 (4)
0.08*D + 0.08*B = 1360 (5)
Now subtract equation (5) from equation (4). You will get
0.02*B = 100,
B = = 9000.
Add equations (2) and (3). You will get
0.08*D + 0.1B = 1460 (4)
Substitute A = 9000 into equation (1), You will get
D + B = 26000 - 9000,
D + B = 17000 (5)
So, now the problem is reduced from 3 unknowns to 2 unknowns
0.08*D + 0.1*B = 1460 (4)
D + B = 17000 (5)
Solve by elimination. For it, multiply equation (5) by 0.08 (both sides ).
0.08*D + 0.1* B = 1460 (4)
0.08*D + 0.08*B = 1360 (5)
Now subtract equation (5) from equation (4). You will get
0.02*B = 100,
B = 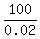 = 5000.
Finally, from equation (1), D = 26000 - 9000 - 5000 = 12000.
ANSWER. A = 9000; B = 5000; D = 12000. = 5000.
Finally, from equation (1), D = 26000 - 9000 - 5000 = 12000.
ANSWER. A = 9000; B = 5000; D = 12000.
Solved.
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We don't know what you mean when you say to solve the problem using matrices. That might mean using a calculator like a TI-83 or TI-84; it might mean using the Gauss-Jordan method; or it might mean using Cramer's rule.
Since we don't know what method you wanted us to use, I won't use matrices at all. And indeed you learn a lot more about solving problems by using an algebraic method.
Here is how I would work the problem, after looking at the given information and considering different possible approaches.
Note that, for a purely algebraic solution, I looked for a way to set the problem up using a single variable, which nearly always makes solving the problem easier.
Let x be the amount of interest from the savings account
Then x+460 is the amount of interest from the CD and bonds
The total interest is $1000:



The amount of interest from the savings account was $270. Since the savings account earned 3% interest, the amount invested in the savings account was $9000.
So the other $17,000 was invested in the CD and the bonds, yielding $730 interest.
The CD earned 4% interest and the bonds earned 5% interest. So a standard formal algebraic solution would start something like this:
let x be the amount invested in the CDs at 4%
then 17000-x is the amount invested in bonds at 5%
The total interest from those two investments was $730:

I leave it to you to finish the problem by that method.
I prefer an informal method for finishing the problem, like this:
All $17000 invested at 4% would have yielded $680 interest; all at 5% would have yielded $850 interest.
The actual interest amount was $730, which is 50/170 = 5/17 of the way from $680 to $850.
That means 5/17 of the remaining $17,000 was invested at the higher rate.
5/17 of $17,000 is $5000; so $5000 was invested in the bonds and the other $12,000 in the CD.
ANSWERS:
$9000 at 3% (savings account)
$12000 at 4% (CD)
$5000 at 5% (bonds)
CHECK: .03(9000)+.04(12000)+.05(5000) = 270+480+250 = 1000
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
|
|
|
| |