Lesson Determinant of a 2x2-matrix and the area of a parallelogram and a triangle

Algebra ->  Matrices-and-determiminant -> Lesson Determinant of a 2x2-matrix and the area of a parallelogram and a triangle      Log On


   

This Lesson (Determinant of a 2x2-matrix and the area of a parallelogram and a triangle) was created by by ikleyn(52756) About Me : View Source, Show
About ikleyn:

Determinant of a 2x2-matrix and the area of a parallelogram and a triangle


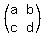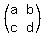You just learned that the determinant of a matrix  A = %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29  is equal to ad+-+bc: det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29 = ad+-+bc  (see,  for example,  the lesson  Determinant of a 2x2-matrix  under the current topic in this site).  Determinants of  2x2-matrices have a remarkable geometric interpretation.

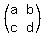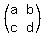Let  A = %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29  be a  2x2-matrix.  Then the modulus  (the absolute value)  of the determinant of the matrix  A,  |det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29|,  is equal to the area of the parallelogram
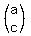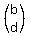which is built in a coordinate plane on vectors  u = %28matrix%282%2C1%2C+a%2C+c%29%29  and  v = %28matrix%282%2C1%2C+b%2C+d%29%29  that are the columns of the matrix  A.

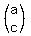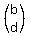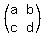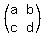Conversely,  if  u = %28matrix%282%2C1%2C+a%2C+c%29%29  and  v = %28matrix%282%2C1%2C+b%2C+d%29%29  are vectors in a coordinate plane,  then the area of the parallelogram which is built on these vectors as on sides is equal to the modulus of the determinant,  |det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29|,  of the  2x2-matrix  A = %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29  whose columns are the given vectors.
Proof
On vectors,  coordinate planes and the vectors on a coordinate plane see the lessons  Vectors in a plane  and  Vectors in a coordinate plane  under the topic  Introduction to vectors, addition and scaling  of the section  Algebra-II  in this site.

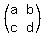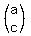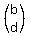Let  A = %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29  be a  2x2-matrix and  u = %28matrix%282%2C1%2C+a%2C+c%29%29  and  v = %28matrix%282%2C1%2C+b%2C+d%29%29  be the vectors in a coordinate plane              
with the coordinates from the first and the second columns of the matrix  A  respectively
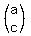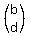(Figure 1).  The vectors  u = %28matrix%282%2C1%2C+a%2C+c%29%29  and  v = %28matrix%282%2C1%2C+b%2C+d%29%29  have the common starting point at the origin  O  of
the coordinate plane.  Let  OBCD  be the parallelogram built on the vectors  u  and  v  as on its sides.

If the vector  u  is turned at the angle  alpha  counterclockwise to the axis  x  then
    a = abs%28u%29%2Acos%28alpha%29,  c = abs%28u%29%2Asin%28alpha%29,  cos%28alpha%29 = a%2Fsqrt%28a%5E2+%2B+c%5E2%29,  sin%28alpha%29 = c%2Fsqrt%28a%5E2+%2B+c%5E2%29.          (1)
Similarly,  if the vector  v  is turned at the angle  beta  counterclockwise to the axis  x  then
    b = abs%28v%29%2Acos%28beta%29,  d = abs%28v%29%2Asin%28beta%29,  cos%28beta%29 = b%2Fsqrt%28b%5E2+%2B+d%5E2%29,  sin%28beta%29 = d%2Fsqrt%28b%5E2+%2B+d%5E2%29.          (2)

            
Figure 1. Vectors  u  and  v  in a coordinate plane
and the parallelogram  OBCD  built on them

It is well known fact from  Geometry  that the area of a parallelogram is equal to the product of the measures of its two adjacent sides and the sinus of the angle between them:
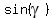    S = abs%28u%29.abs%28v%29.sin%28gamma%29.              (3)
See,  for example,  the lesson  Area of a parallelogram  under the topic  Area and surface area  of the section  Geometry  in this site.
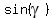The angle  gamma  in the formula  (3)  is the angle concluded between  0  and  pi,  so that  sin%28gamma%29  is always positive.

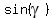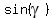Notice that the angle  gamma between the vectors  u  and  v  is equal to  beta-alpha,  or  -%28beta-alpha%29,  or  2pi+-+%28beta-alpha%29,  depending on the situation.  But in any case,  sin%28gamma%29  is equal to the modulus of  sin%28beta-alpha%29,  sin%28gamma%29 = abs%28sin%28beta-alpha%29%29,  and has a positive  (non-negative)  value.

Now,  sin%28beta-alpha%29 = sin%28beta%29%2Acos%28alpha%29+-+cos%28beta%29%2Asin%28alpha%29,  in accordance with the subtraction formula for sinus from  Trigonometry  (see the lesson  Addition and subtraction formulas  in this site).  By substituting the values of  sin%28beta%29,  cos%28alpha%29,  cos%28beta%29 and  sin%28alpha%29  from  (1)  and  (2),  you will get

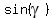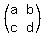S = abs%28u%29.abs%28v%29.sin%28gamma%29 = abs%28u%29.abs%28v%29.|d%2Fsqrt%28b%5E2+%2B+d%5E2%29.a%2Fsqrt%28a%5E2+%2B+c%5E2%29 - b%2Fsqrt%28b%5E2+%2B+d%5E2%29.c%2Fsqrt%28a%5E2+%2B+c%5E2%29| = sqrt%28a%5E2%2Bc%5E2%29.sqrt%28b%5E2%2Bd%5E2%29.|d%2Fsqrt%28b%5E2+%2B+d%5E2%29.a%2Fsqrt%28a%5E2+%2B+c%5E2%29 - b%2Fsqrt%28b%5E2+%2B+d%5E2%29.c%2Fsqrt%28a%5E2+%2B+c%5E2%29| = |ad - bc| = |det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29|.

It is what has to be proved.


Example 1

Find the area of a parallelogram in a coordinate plane with one vertex at the origin if its sides released from this vertex are the vectors with coordinates  u = (2,1)  and  v = (1,2).

Solution

The area of this parallelogram is equal to the modulus of the determinant of the  2x2-matrix  %28matrix%282%2C2%2C+2%2C1%2C1%2C2%29%29:  S = |det %28matrix%282%2C2%2C+2%2C1%2C1%2C2%29%29| = |2%2A2+-+1%2A1| = |3| = 3.


Example 2

Find the area of a parallelogram in a coordinate plane with one vertex at the origin if its sides released from this vertex are the vectors with coordinates  u = (1,3)  and  v = (3,1).

Solution

The area of this parallelogram is equal to the modulus of the determinant of the  2x2-matrix  %28matrix%282%2C2%2C+1%2C3%2C3%2C1%29%29:  S = |det %28matrix%282%2C2%2C+1%2C3%2C3%2C1%29%29| = |1%2A1+-+3%2A3| = |-8| = 8.



There is similar connection between determinants of  2x2-matrices and the areas of triangles.

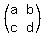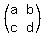Let  A = %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29  be a  2x2-matrix.  Then the modulus  (the absolute value)  of the determinant of the matrix  A,  |det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29|,  is equal to the doubled area of the triangle
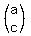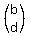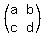which is built in a coordinate plane on vectors  u = %28matrix%282%2C1%2C+a%2C+c%29%29  and  v = %28matrix%282%2C1%2C+b%2C+d%29%29  that are the columns of the matrix  A:  |det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29| = 2S%5BDELTA%5D.

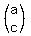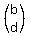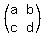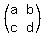Conversely,  if  u = %28matrix%282%2C1%2C+a%2C+c%29%29  and  v = %28matrix%282%2C1%2C+b%2C+d%29%29  are vectors in a coordinate plane,  then the area of the triangle which is built on these vectors as on sides is equal to the half of the modulus of the determinant,  |det %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29|,  of the  2x2-matrix  A = %28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29  whose columns are the given vectors:  S%5BDELTA%5D = 1%2F2.|det %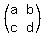28matrix%282%2C2%2C+a%2C+b%2C+c%2C+d%29%29|.

This is an immediate corollary of the two statements proved in the first part of the lesson.                    
Indeed,  the area of each mentioned triangle is half of the area of the parallelogram which
is build on the given vectors  (Figure 2).


Example 3

Find the area of a triangle in a coordinate plane with one vertex at the origin
if its sides released from this vertex are the vectors with coordinates  u = (2,1)  and  v = (1,2).

            
Figure 2. Vectors  u  and  v  in a coordinate plane,
the triangle  OBD  and the parallelogram  OBCD  built on them

Solution

The area of this triangle is half of the modulus of the determinant of the  2x2-matrix  %28matrix%282%2C2%2C+2%2C1%2C1%2C2%29%29:  S%5BDELTA%5D = 1%2F2.|det %28matrix%282%2C2%2C+2%2C1%2C1%2C2%29%29| = 1%2F2.|2%2A2+-+1%2A1| = |3%2F2|.


Example 4

Find the area of a triangle in a coordinate plane with one vertex at the origin if its sides released from this vertex are the vectors with coordinates  u = (1,3)  and  v = (3,1).

Solution

The area of this triangle is half of the modulus of the determinant of the  2x2-matrix  %28matrix%282%2C2%2C+1%2C3%2C3%2C1%29%29:  S%5BDELTA%5D = 1%2F2.|det %28matrix%282%2C2%2C+1%2C3%2C3%2C1%29%29| = 1%2F2.|1%2A1+-+3%2A3| = |-8%2F2| = 4.


My other lessons on matrices, determinants of 2x2-matrices and the Cramer's rule for systems of linear equations in two unknowns in this site are
    - What is a Matrix?,
    - Determinant of a 2x2-matrix,
    - HOW TO solve system of linear equations in two unknowns using determinant (Cramer's rule),
    - Solving systems of linear equations in two unknowns using the Cramer's rule,
    - Solving word problems by the Cramer's rule after reducing to systems of linear equations in two unknowns,
    - Solving systems of non-linear equations in two unknowns using the Cramer's rule  and
    - OVERVIEW of LESSONS on determinants of 2x2-matrices and Cramer's rule for systems in 2 unknowns
under the current topic  Matrices, determinant, Cramer rule  of the section  Algebra-II.


Use this file/link  ALGEBRA-II - YOUR ONLINE TEXTBOOK  to navigate over all topics and lessons of the online textbook  ALGEBRA-II.

This lesson has been accessed 9538 times.