A.)
3|3x+4|-7 = 5
We must isolate the |3x+4|
Add 7 to both sides
3|3x+4| = 12
Divide both sides by 3
|3x+4| = 4
[This has a solution because an absolute value can
equal to a positive number. Always make that
observation because when there is a negative number
on the right side of the equation, there is no
solution, as your next problem illustrates]
To get rid of the absolute value bars, split into two
equations
3x+4 = 4; 3x+4 = -4
3x = 0; 3x = -8
x = 0; x =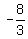 
------------------------------------------
B.)
2|2x-1| = -4
We must isolate the |2x-1|.
So we divide both sides by 2 to isolate |2x-1|
|2x-1| = -4
We observe from this step that there is no solution,
because an absolute value is never negative, and here
we have an absolute value equaling to a negative number,
-4. So there is no solution. Do not continue any
absolute value equation when there is an absolute value
on one side and a negative number on the other. If you
continue you may get an answer but the answer will be
wrong.
Edwin
