SOLUTION: Maximize 3x + 2y Subject to the constraints 5x + 3y <= 15 3x + 4y <= 12 x,y >= 0

Question 1114893: Maximize 3x + 2y
Subject to the constraints
5x + 3y <= 15
3x + 4y <= 12
x,y >= 0
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
using the desmos.com calcculator, graph the opposite of these inequalities.

the area of the graph that is not shaded is your region of feasibility.

your maximum value for 3x + 2y will be at one of corner points of your region of feasibility.

the graph is shown below:

$$$

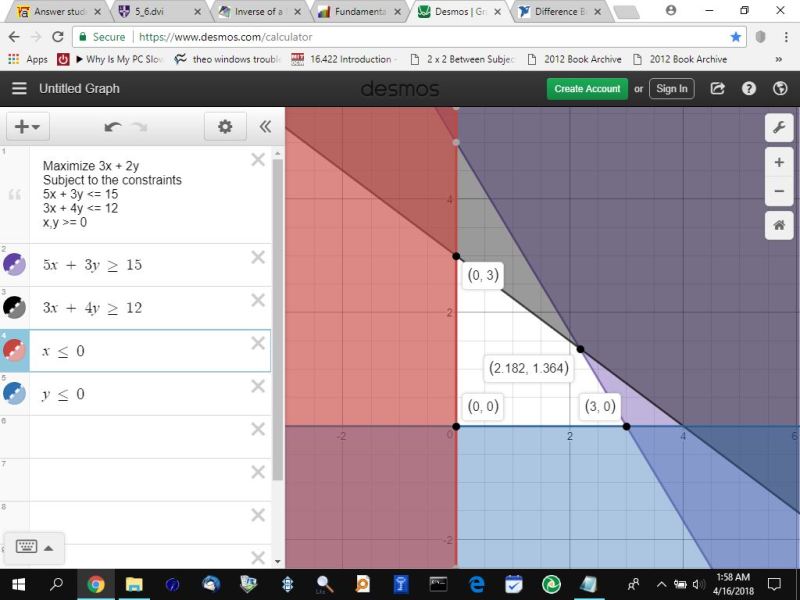
at (0,3), 3x + 2y = 3*0 + 2*3 = 6
at (2.182,1.364) 3x + 2y = 3*2.182 + 2*1.364 = 9.274
at (3,0), 3x + 2y = 3*3 + 2*0 = 9

your maximum solution is at (2.182,1.364).

RELATED QUESTIONS
Maximize 5x + 3y Subject to the constraints 5x + 2y <= 40 3x + 6y <= 48 x <= (answered by Fombitz)

Maximize z = 2x + 4y subject to the constraints x ≥ 0, y ≥... (answered by Edwin McCravy)

Maximize z = 2x + 4y subject to the constraints x ≥ 0, y ≥ 0, x + y (answered by solver91311)

Use the simplex method to maximize p= 5x+4y+3z subject to the constraints: x>=0, y>=0,... (answered by Edwin McCravy)

Maximize P=3x + 2y Subject to 2x +3y ≤ 12 (answered by math_tutor2020)

Maximize z = 3x + 5y subject to the constraints x ≥ 0, y ≥... (answered by jsmallt9)

Maximize z = 3x + 5y subject to the constraints x ≥ 0, y ≥... (answered by solver91311,jsmallt9)

Maximize z = 3x + 5y subject to the constraints x ≥ 0, y ≥... (answered by jsmallt9)

Maximize p = 5x + 3y subject to 2x + 3y <= 12 3x + y >= 16 x + y >= 3 2x + y >=... (answered by KMST)