SOLUTION: I just want to check if my answer is correct.
Problem: The center of the circle is at (-3,-2). If a chord of length 4 is bisected at (3,1), find the length of the radius.
My
Algebra.Com
Question 924004: I just want to check if my answer is correct.
Problem: The center of the circle is at (-3,-2). If a chord of length 4 is bisected at (3,1), find the length of the radius.
My answer is: 3√6
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
based on the following, your radius has to be perpendicular to the chord.
http://www.regentsprep.org/regents/math/geometry/gp14/circlechords.htm
so you get a triangle formed by the radius of the circle and the chord such that the ends of the chord that connect to the center of the circle are each a radius of the circle.
the chord is 4 units in length.
two right triangles are formed with each right triangle having a base of 2 which is 1/2 the length of the chord.
the length of the line segment formed by the radius that bisects the chord is found by taking the 2 points common to that radius and finding the distance between them.
the two points are (-3,-2) and (3,1)
the distance between them will be square root of [(-2-1)^2 + (-3-3)^2] which becomes square root of [9 + 36] which becomes square root of (45).
your right triangle has one leg of 2 and one leg of sqrt(45)
to find the hypotenuse of the right triangle which is the radius of the circle, you need to use the pythagorean formula.
you will get r^2 = 2^2 + sqrt(45)^2
that becomes r^2 = 4 + 45 which makes r^2 = 49 which makes r = 7.
the radius of your circle has to be 7.
the equation of your circle becomes:
(x+3)^2 + (y + 2)^2 = 49
a graph of the circle and the chord and the radius that bisects the chord is shown below:
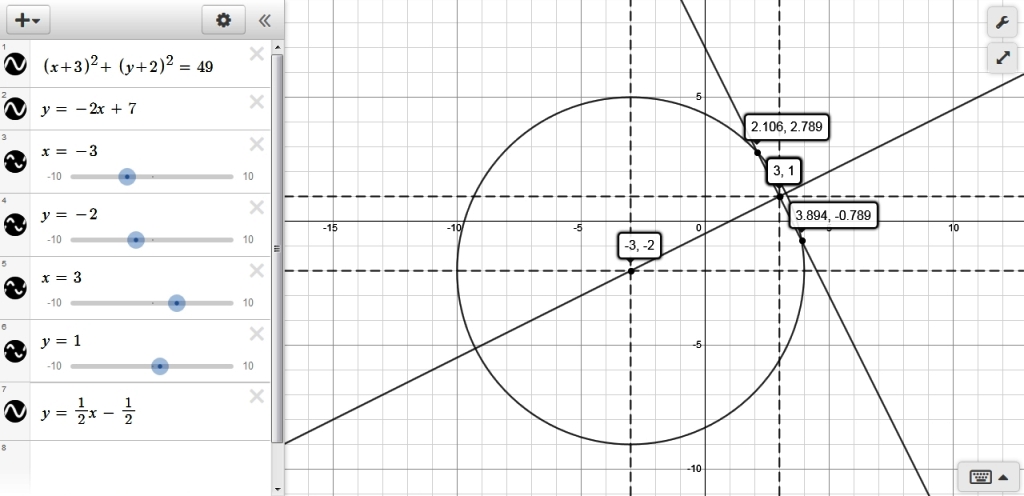
all the numbers check out.
the radius is 7
each sice of the chord that is bisected by the radius has a length of 2.
RELATED QUESTIONS
I just want to check if my answer is correct.
Problem:the center of the circle is at... (answered by rothauserc)
I just want to check if my answer is correct.
Problem: The center of the circle is at... (answered by josgarithmetic)
I just want to check if my answer is correct.
The problem is: Find the center of the... (answered by jim_thompson5910,MathTherapy)
if a diameter of a circle does not bisect a chord, is it perpendicular to the... (answered by dabanfield)
hi, i need your help please... i don't know how to answer these questions because i can't (answered by Theo)
If the distance from center of a circle to a chord is 5 and the length of chord is 24.... (answered by lwsshak3)
a chord of a circle is 4 inches from the center. If the diameter of the circle is 10... (answered by smash)
a chord of a circle is 4 inches from the center. If the diameter of the circle is 10... (answered by Edwin McCravy)
A chord of a circle is 4 inches from the center. If the diameter of the circle is 10... (answered by tazoftroy)
