|
Question 682613: if two vertices of an equilateral triangle are (-4,3) and(0,0), find the third vertex.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is one side of the equilateral triangle:
 And as you can see there are two solutions. Let the third
vertex be (a,b):
And as you can see there are two solutions. Let the third
vertex be (a,b):
 and and First we find the distance from (0,0) to (-4,3) by the distance formula:
d =
First we find the distance from (0,0) to (-4,3) by the distance formula:
d = 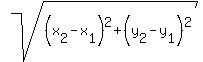 d =
d = 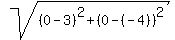 d =
d =  d =
d = 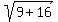 d =
d = 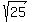 d = 5
So we know the distance from (0,0) to (a,b) must equal 5
so that the triangle will be equilateral. So we use the
distance formula to make that equation:
d = 5
So we know the distance from (0,0) to (a,b) must equal 5
so that the triangle will be equilateral. So we use the
distance formula to make that equation:
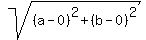 = 5 = 5
 = 5
Square both sides:
a² + b² = 25
We also know the distance from (-4,3) to (a,b) must also
equal 5 so that the triangle will be equilateral. So we
use the distance formula again to make that equation: = 5
Square both sides:
a² + b² = 25
We also know the distance from (-4,3) to (a,b) must also
equal 5 so that the triangle will be equilateral. So we
use the distance formula again to make that equation:
 = 5 = 5
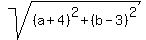 = 5
Square both sides:
(a+4)² + (b-3)² = 25
a² + 8a + 16 + b² - 6b + 9 = 25
a² + 8a + b² - 6b + 25 = 25
a² + 8a + b² - 6b = 0
So we have the system of equations:
a² + b² = 25
a² + 8a + b² - 6b = 0
Subtracting the second equation from the first equation
gives the equation:
-8a + 6b = 25
6b = 25 + 8a
b = = 5
Square both sides:
(a+4)² + (b-3)² = 25
a² + 8a + 16 + b² - 6b + 9 = 25
a² + 8a + b² - 6b + 25 = 25
a² + 8a + b² - 6b = 0
So we have the system of equations:
a² + b² = 25
a² + 8a + b² - 6b = 0
Subtracting the second equation from the first equation
gives the equation:
-8a + 6b = 25
6b = 25 + 8a
b = 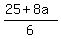 Substitute in
a² + b² = 25
a² +
Substitute in
a² + b² = 25
a² + 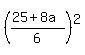 = 25
a² + = 25
a² +  = 25
Multiply thru by 36 to clear of fractions:
36a² + (25 + 8a)² = 900
36a² + 625 + 400a + 64a² = 900
100a² + 400a - 275 = 0
Divide thru by 25
4a² + 16a - 11 = 0
Use the quadratic formula:
a = = 25
Multiply thru by 36 to clear of fractions:
36a² + (25 + 8a)² = 900
36a² + 625 + 400a + 64a² = 900
100a² + 400a - 275 = 0
Divide thru by 25
4a² + 16a - 11 = 0
Use the quadratic formula:
a =  a =
a = 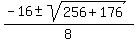 a =
a = 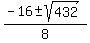 a =
a = 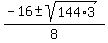 a =
a = 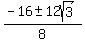 a =
a = 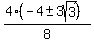 a =
a = 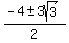 Substituting in
6b = 25 + 8a
6b = 25 + 8(
Substituting in
6b = 25 + 8a
6b = 25 + 8(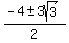 )
6b = 25 + 4(-4 +- 3 )
6b = 25 + 4(-4 +- 3 )
6b = 25 - 16 +- 12 )
6b = 25 - 16 +- 12 )
6b = 9 ± 12 )
6b = 9 ± 12 )
Divide through by 3
2b = 3 ± 4 )
Divide through by 3
2b = 3 ± 4 b =
b = 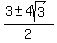 So the third coordinate has two solutions:
(a,b) = (
So the third coordinate has two solutions:
(a,b) = (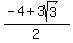 , , 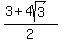 )
and
(a,b) = ( )
and
(a,b) = (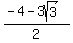 , , 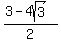 )
These are approximately:
(a,b) = (0.598, 4.964) and
(a,b) = (-4.598, -1.964)
Edwin )
These are approximately:
(a,b) = (0.598, 4.964) and
(a,b) = (-4.598, -1.964)
Edwin
|
|
|
| |