Hi, I'm having a difficult time figuring this problem out. THANKS FOR HELPING!!
Find the longest and shortest line segment drawn in
the following diagram.
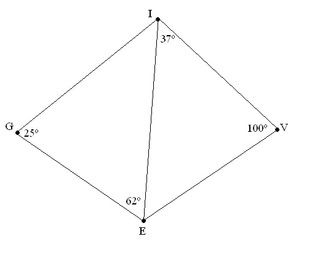
Hi, I'm having a difficult time figuring this problem out. THANKS FOR HELPING!!

Hi, I'm having a difficult time figuring this problem out. THANKS FOR HELPING!! Find the longest and shortest line segment drawn in the following diagram.The sides of a triangle are always in the same order of size as the angles opposite them: First we calculate the two angles we aren't given by using the fact that the three angles of any triangle must always have sum 180° ŠG + ŠEIG + ŠGEI = 180° 25° + ŠEIG + 62° = 180° 87° + ŠEIG = 180° ŠEIG = 93° ŠV + ŠEIV + ŠIEV = 180° 100° + 37° + ŠIEV = 180° 137° + ŠIEV = 180° ŠIEV = 43° In DEGI, ŠG < ŠGEI < ŠEIG, so their opposite sides are respectively in the same order: EI < GI < EG In DEIV, ŠEIV < ŠIEV < ŠV, so their opposite sides are respectively in the same order: EV < IV < EI So we can put those two inequalities together, and get EV < IV < EI < GI < EG Therefore EV is the shortest side and EG is the longest side. Edwin
find the principal root __(answered by Edwin McCravy)
add and/or subtract and simplify the following radical...(answered by checkley71,AnlytcPhil)
cosq = 5/12 and tanq is(answered by AnlytcPhil)
mŠ1:mŠ2 = 1:5. Find...(answered by Edwin McCravy)
Find the exact values for the trig functions, with the radian measure:
(answered by venugopalramana,AnlytcPhil)I need help with this. Simplify the expression Simplify the expression. __(answered by Nate,AnlytcPhil)
Let a and b be acute...(answered by AnlytcPhil)