SOLUTION: Find the exact directed distance from the line 3x-4y=12 to the point (-2,-1).

Use the formula:

The distance from the line Ax+By+C=0 to the point (h,k) is given
by the formula

d = ± where the sign is the sign
of  

For your equation

3x-4y=12, first get 0 on the right:

3x-4y-12=0

Then compare to

Ax+By+C=0

and get A=3, B=-4, C=-12, and (h,k) = (-2,-1), so h=-2 and k=-1

 =  =  which is negative, so the
directed distance will be negative:

Substituting:

d = ±

d = -

d = -

d = -

d = -

d = -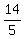 = -2.8

And that green line looks a little shorter than 3 units long.
That's only a "ballpark" check. But if you compare it to 3
units along the x-axis or the y-axis, you'll agree that 2.8
is at least close to the length of that green line.

Edwin