|
Question 1197813: The line joining ( -8, 1 ) and ( 11, 7 ) is divided into four equal parts. Find the points of division.
Found 2 solutions by josgarithmetic, math_tutor2020:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Refer to this lesson
https://www.algebra.com/algebra/homework/formulas/split-segment-n-pieces.lesson
because I'll be using the formula mentioned there. I show how the formula is derived.
In this case,
(a,b) = (-8,1)
(c,d) = (11,7)
are the two endpoints
We want to split the segment into n = 4 pieces.
So
deltaX = (1/n)*|c-a|
deltaX = (1/4)*|11-(-8)|
deltaX = 19/4
deltaX = 4.75
This is the increment we move along the horizontal axis when determining each cutoff point.
Furthermore,
xm = a + m*deltaX
xm = -8 + m*4.75
xm = 4.75m - 8
where m is an integer in the interval 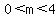
When I write xm, I really mean "x subscript m" or 
And
deltaY = (1/n)*|d-b|
deltaY = (1/4)*|7-1|
deltaY = 6/4
deltaY = 1.5
This is the increment we move along the vertical axis when determining each cutoff point.
Furthermore,
ym = b + m*deltaY
ym = 1 + m*1.5
ym = 1.5m + 1
------------------------------------------------------------
We have this so far
xm = 4.75m - 8
ym = 1.5m + 1
So,
(xm,ym) = (4.75m-8, 1.5m+1)
where m is an integer such that 0 < m < 4
This represents the general form of our cutoff points.
We'll plug in integer values from m = 1 to m = 3.
For example, if m = 1, then...
xm = 4.75m-8
x1 = 4.75*1-8
x1 = 4.75-8
x1 = -3.25
ym = 1.5m+1
y1 = 1.5*1+1
y1 = 1.5+1
y1 = 2.5
This gives one cutoff point at (x1,y1) = (-3.25,2.5)
This is point B shown below.
If m = 2, then,
xm = 4.75m-8
x2 = 4.75*2-8
x2 =9.5-8
x2 = 1.5
ym = 1.5m+1
y2 = 1.5*2+1
y2 = 3+1
y2 = 4
This gives another cutoff point at (x2,y2) = (1.5,4)
This is point C shown below.
Here's a table of values to keep things organized.
Spreadsheet software is recommended to not only keep things organized, but to also quickly compute each (xm,ym) cutoff point.
| m | xm = 4.75m-8 | ym = 1.5m+1 | (xm,ym) | Point | | 1 | -3.25 | 2.5 | (-3.25,2.5) | B | | 2 | 1.5 | 4 | (1.5,4) | C | | 3 | 6.25 | 5.5 | (6.25,5.5) | D |
Here's what the graph looks like

The answer points are marked in red.
A = (-8,1) is one endpoint
B = (-3.25,2.5)
C = (1.5,4)
D = (6.25,5.5)
E = (11,7) is the other endpoint
------------------------------------------------------------
To confirm the answers, use the distance formula to show the following
AE = sqrt(397)
AB = sqrt(24.8125)
BC = sqrt(24.8125)
CD = sqrt(24.8125)
DE = sqrt(24.8125)
This will show that AB=BC=CD=DE and that segment AE has been cut into four equal pieces.
I'll let the student do these steps for the confirmation.
Note:
AE = 4*AB
sqrt(397) = 4*sqrt(24.8125)
Another way to confirm the answers is to use something like GeoGebra.
Yet another confirmation method is to use the midpoint formula on endpoints A and E, and it will pinpoint where C is located.
Then use the midpoint formula on A and C to find where B is located.
Finally, use the midpoint formula on C and E to find where D is located.
This repeated midpoint trick only works when there are 2^k equal pieces, where k is some positive integer.
|
|
|
| |