SOLUTION: The weight of a body at or above the earths surface varies inversely as the square of the distance from the earths center. What does a 450 kg object weigh 500 km away for the earth

That says:



>>...a 450 kg object weighs 4410 Newtons 
at the surface of the earth...<<

On the surface of the earth the distance d 
to the center of the earth is 6500 km, so
when d = 6500, then W = 4410. We substitute
that in the equation:





Now we can solve for k. So we multiply both 
sides by .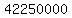





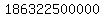So we substitute  for  in





Now we read the question:

Since it's 500 km above the earth and it's 6500 km 
from the surface down to center of the earth, 
then the object is 500+6500 or 7000 km from 
the center of the earth.  So when d = 7000km,
we want to know what W is when d is 7000.


 




So it weighs 3802.5 Newtons.

Edwin