SOLUTION: Let f(x) = (x-8)^2 Find a domain on which f is one to one and non decreasing Answer= [8,oo) BUT What is the inverse of f restricted to this domain?? f^-1(x)=?

Question 1093996: Let f(x) = (x-8)^2
Find a domain on which f is one to one and non decreasing
Answer= [8,oo) BUT
What is the inverse of f restricted to this domain??
f^-1(x)=?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
set y = (8-x)^2

replace y with x and x with y to get:

x = (8-y)^2

solve for y as follows:

take square root of both sides to get plus or minus sqrt(x)= 8-y.

this give you two equations.

plus sqrt(x) = 8 - y.

minus sqrt(x) = 8 - y

add y to both sides of the first equation and subtract sqrt(x) from both sides of the first equation to get:

y = 8 - sqrt(x)

add y to both sides of the second equation and add sqrt(x) to both sides of the second equation to get:

y = 8 + sqrt(x)

these are your inverse equations.

you need to apply the test for inverse euation to see which is inverse for what.

when x > 8, then if f(x) = (x,y), then f^-1)(x) = (y,x)

so take a value of x greater than 8, say 12, and solve for y = (8-x)^2.

you will get y = (8-12)^2 = (-4)^2 = 16.

your coordinate point of the regular function is (12,16).

now take y = 8 + sqrt(x) and replace x with 16 and solve for y.

you will get y = 8 + sqrt(16) = 8 + 4 = 12.

your coordinate point of the inverse function is (16,12).

y = 8 + sqrt(x) is your inverse function to the part of y = (8-x)^2 that is increasing.

graphically, it looks like this:

$$$

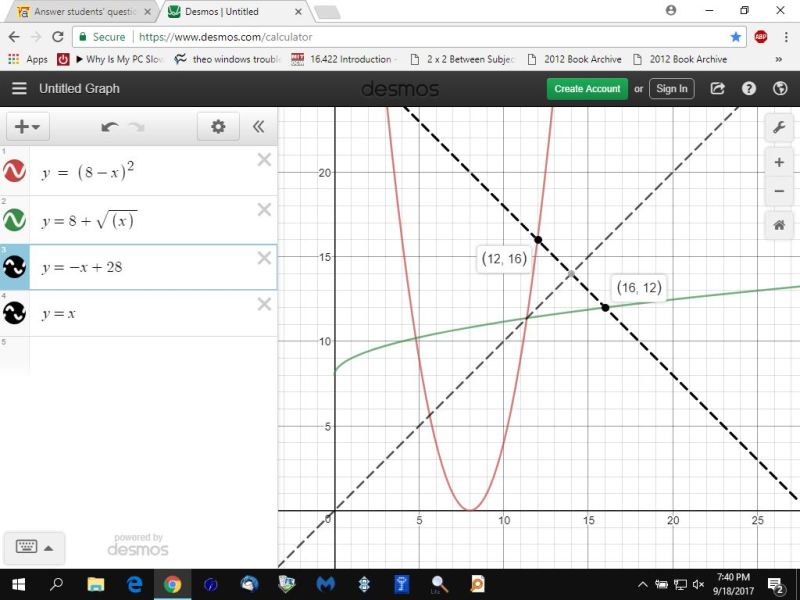
the inverse function is a reflection about the line y = x.

(x,y) in the original graph is reflected by (y,x) in the inverse graph.

this is clearly seen in the graph.

RELATED QUESTIONS
Let f ( x ) = ( x − 4 )^2 Find a domain on which f is one-to-one and non-decreasing. (answered by MathLover1)

Question 3.7/10 Let f(x)=(x-5)2 Find a domain on which f is one-to-one and... (answered by MathLover1)

Question 3.7/9 Let f(x)=(x+1)2 Find a domain on which f is one-to-one and... (answered by MathLover1)

Question 3.7/12 Let f(x)=(x+1)2 Give the largest domain on which f is one-to-one... (answered by KMST)

Let f(x) = (x - 5)^2 Find a domain on which f is one-to-one and increasing. Use oo... (answered by Boreal)

Let f(x) = (x-2)^3+8 a. Show that this function is one-to-one algebraically. b. Find... (answered by htmentor)

1)The equation defines a one-to-one function f. Determine f -1 and verify that f f -1... (answered by solver91311)

if F is one-to-one, find equation for its inverse... (answered by funmath)

The one-to-one function is defined by f(x) = x/(8-9x) Find f^-1, the inverse of f... (answered by stanbon,Theo)