replace x with y and y with x to get:
x = y + sqrt(y).
that is your inverse equation.
you could use that equation and you would be fine.
some graphing software would allow you to graph it that way.
most others require you to solve for y.
if you graphed it manually, you could also graph it as is.
the problem comes when you want to solve the equation of x = y + sqrt(y) for y.
i stumbled on to a method that i believe works.
you get an equivalent equation when x is greater than or equal to 0.
start with y = x + sqrt(x)
replace y with x and x with y to get:
x = y + sqrt(y)
that is your inverse equation.
now to solve it for y
start with y + sqrt(y) = x
let z = sqrt(y)
your equation of y + sqrt(y) = x now becomes:
z^2 + z = x
z^2 + z is equivalent to (z + 1/2)^2 -1/4
you can determine they're equivalent by evaluating (z + 1/2)^2 - 1/4
you will get z^2 + z + 1/4 - 1/4 = z^2 + z
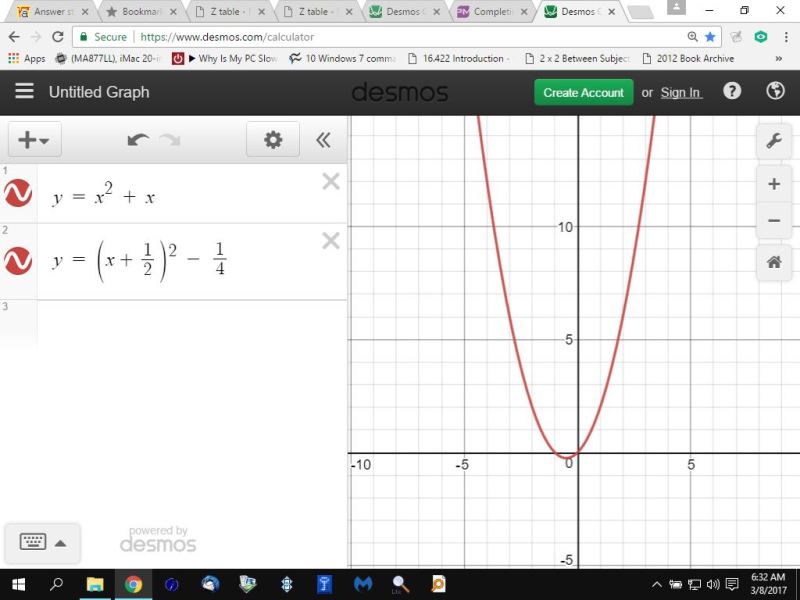
i can also show you graphically they're equivalent by graphing both y = x^2 + x and y = (x + 1/2)^2 - 1/4
the results of graphing both those equations is shown below:
you can see that both of those equations are equivalent because they make the same graph.
if they were different equations, they would show up as two separate graphs.
only one is shown so both equations make the same graph which confirms that the equations are equivalent to each other and one can be replaced by the other any time you like.
this is done by using the completing the square method of factoring a quadratic equation.
a reference on that can be found here:
http://www.purplemath.com/modules/sqrquad.htm
so, ......
your equation of x = y + sqrt(y) becomes:
y + sqrt(y) = x
let sqrt(x) = y and the equation becomes:
z^2 + z = x
factor z^2 + z using the completing the square method and the equation becomes:
(z+1/2)^2 - 1/4 = x
add 1/4 to both sides of the equation to get:
(z + 1/2)^2 = x + 1/4
take the square root of both sides of the equation to get:
z + 1/2 = sqrt(x + 1/4)
subtract 1/2 from both sides of the equation to get:
z = sqrt(x + 1/4) - 1/2
since z = sqrt(y), replace z with sqrt(y) to get:
sqrt(y) = sqrt(x + 1/4) - 1/2
square both sides of the equation to get:
y = (sqrt(x+ 1/4) - 1/2)^2
that's your inverse equation of x = y + sqrt(y) after you solved for y.
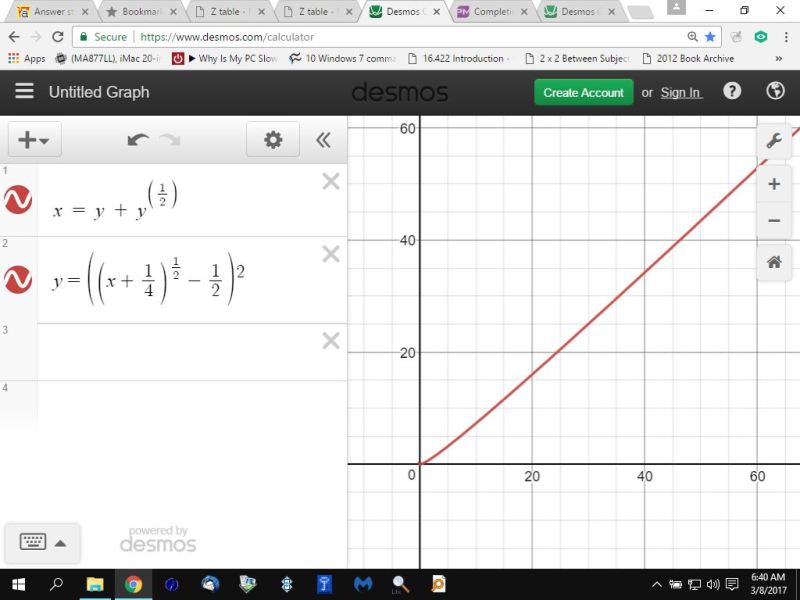
the following graph shows you that x = y + sqrt(y) and y = (sqrt(x + 1/4) - 1/2)^2 are equivalent equations when x is greater than or equal to 0.
the following graph shows you that y = (sqrt(x+ 1/4) - 1/2)^2 is the inverse equation of y = x + sqrt(x) when the value of x is greater than or equal to 0.
you can see that the equations are mirror images about the line y = x.
you can also see that (x,y) in the original equation is equal to (y,x) in the inverse equation.
this is shown by the points (.25,.75) and (.75,.25).
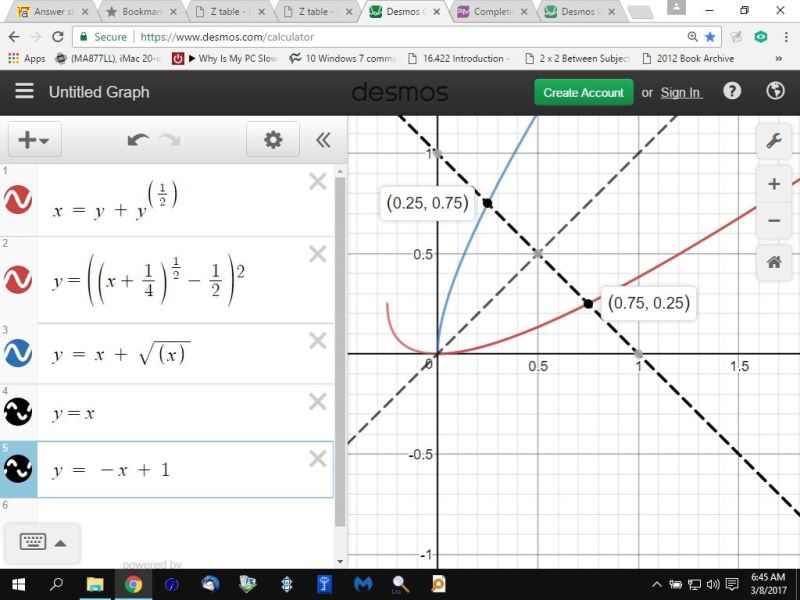
the restriction when x is greater than or equal to 0 is necessary since the graph of x = y + sqrt(y) doesn't go below x = 0 while the graph of y = (sqrt(x + 1/4) - 1/2)^2 does.