|
This Lesson (Solving problems on quadratic inequalities) was created by by ikleyn(52748)   : View Source, ShowAbout ikleyn:
Solving problems on quadratic inequalities
In this lesson you will find the solutions of typical problems on quadratic inequalities:
1)  >=  ; 2)  >= ; 3)  >= ; 4)  >= ; 5)  >= ; 6)  >= ; 7)  >= .
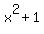Problem 1Solve the quadratic inequality >= .
Solution
The expression is the product of two factors  and  : =  .
If  <=  , both the factors are non-positive, so their product is non-negative: >= .
If < <  , then the factor  is positive and the factor  is negative,
so their product is negative: < .
If >= , both the factors are non-negative, so their product is non-negative: >= .
Thus the quadratic polynomial is non-negative at <= and >= , and this is
the set of real numbers satisfying the given inequality  >= .
|
Fig.1. The factor
and plots
|
Fig.2. The parabola
 = plot
|
Figure 1 shows the plots of the linear factors and separately. Figure 2 shows the plot of the polynomial which is the product of these factors.
It is clearly seen from the Figure 2 that the quadratic polynomial is non-negative outside the interval < < .
Answer. The solution of the given inequality  >= is the union of two semi-infinite segments <= and >= .
Problem 2Solve the quadratic inequality  >= .
Solution
The expression is the product of two factors and taken with the
"minus" sign: =  .
If < , both the factors are negative, so is negative: < .
If <= <= , then the factor is non-negative and the factor is non-positive,
so is non-negative: >= .
If > , both the factors are positive, so is negative: < .
Thus the expression is non-negative at <= <= , and this is the set of real
numbers satisfying the given inequality  >= .
|
Fig.3. The factors
and plots
|
Fig.4. The parabola
= plot
|
Figure 3 shows the plots of the linear factors and separately. Figure 4 shows the plot of the polynomial which is the product of these factors.
It is clearly seen from the Figure 4 that the quadratic polynomial is non-negative on the segment <= <= .
Answer. The solution of the given inequality >= is the segment <= <= .
Problem 3Solve the quadratic inequality >= .
Solution
The left side is the product of two linear factors  and .
If <=  , then both the factors are non-positive, so their product is non-negative: >= .
If < < , then the factor  is positive and the factor is negative,
so their product is negative: < .
If >= , then both the factors are non-negative, so their product is non-negative: >= .
Thus the quadratic polynomial is non-negative at <= and >= , and this is
the set of real numbers satisfying the given inequality >= .
|
Fig.5. The factor
and plots
|
Fig.6. The parabola
= plot
|
Figure 5 shows the plots of the linear factors and separately. Figure 6 shows the plot of the product of these factors .
It is clearly seen from the Figure 6 that the quadratic polynomial is non-negative outside the interval < < .
Answer. The solution of the given inequality  >= is the union of two semi-infinite segments <= and >= .
Problem 4Solve the quadratic inequality >= .
Solution
The left side is the product of two linear factors and  taken with the
"minus" sign: = .
If < , then both the factors are negative, so is negative: < .
If <= <=  , then the factor is non-negative and the factor is non-positive,
so is non-negative: >= .
If > , then both the factors are positive, so is negative: < .
Thus the expression is non-negative at <= <= , and this is the set of real
numbers satisfying the given inequality >= .
|
Fig.7. The factors
and  plots
|
Fig.8. The parabola
= plot
|
Figure 7 shows the plots of the linear factors and separately. Figure 8 shows the plot of the polynomial which is the product of these factors.
It is clearly seen from the Figure 8 that the quadratic polynomial is non-negative on the segment <= <= .
Answer. The solution of the given inequality >= is the segment <= <= .
Problem 5Solve the quadratic inequality  >= .
Solution
The polynomial has the roots  = and  = . (You can get these roots using
the quadratic formula from the lesson PROOF of quadratic formula by completing the square or
using the Viete's theorem of the lesson Solving quadratic equations without quadratic formula).
Therefore, the polynomial is the product of linear factors =  .
You can also check it directly.
If <= , both linear factors are non-positive, so their product is non-negative: >= .
If < < , then the factor is positive and the factor is negative,
so their product is negative: < .
If >= , both the factors are non-negative, so their product is non-negative: >= .
|
Fig.9. The factor
and plots
|
Fig.10. The parabola
= plot
|
Thus the expression is non-negative at <= and >= , and this is the set of real numbers satisfying the given inequality >= .
Figure 9 shows the plots of the linear factors and separately. Figure 10 shows the the plot of the polynomial which is the product of these factors.
It is clearly seen from the Figure 10 that the quadratic polynomial is non-negative outside the interval < < .
Answer. The solution of the given inequality >= is the union of two semi-infinite segments <= and >= .
Problem 6Solve the quadratic inequality >= .
Solution
The polynomial has the roots =  and = . (You can get these roots using
the quadratic formula from the lesson PROOF of quadratic formula by completing the square or
using the Viete's theorem of the lesson Solving quadratic equations without quadratic formula).
Therefore, the polynomial is the product of linear factors (x+1) and (x-3) taken
with the "minus" sign: =  . You can also check it directly.
If < , both the factors are negative, so is negative: < .
If <= <= , then the factor  is non-negative and the factor is non-positive,
so is non-negative: >= .
If > , both the factors are positive, so is negative: < .
|
Fig.11. The factor
and plots
|
Fig.12. The parabola
= plot
|
Thus the expression is non-negative at <= <= and this is the set of real numbers satisfying the given inequality  >= .
Figure 11 shows the plots of the linear factors and separately. Figure 12 shows the plot of the polynomial which is the product of these factors
with the sign "minus". It is clearly seen from the Figure 12 that the quadratic polynomial is non-negative on the segment <= <= .
Answer. The solution of the given inequality >= is the segment <= <= .
Problem 7Solve the quadratic inequality  >= .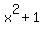
SummaryTo solve a quadratic inequality with a quadratic polynomial on the left side
1) find the real roots of the polynomial;
2) using the roots, write the polynomial as the product of two linear binomials (if it is not presented in this form yet);
3) analyze the sign of each factor and the sign of their product by moving along the number line from left to right.
Determine the sign of the quadratic polynomial in the number line to the left of the smaller root; between the roots; and to the right of the larger root.
4) be aware of special cases. One special case is when the quadratic polynomial has no real roots. Another special case is when two roots of the polynomial coincide.
My other lessons on solving inequalities are
- Solving simple and simplest linear inequalities
- Solving absolute value inequalities
- Advanced problems on solving absolute value inequalities
- Solving systems of linear inequalities in one unknown
- Solving compound inequalities
- What number is greater? Comparing magnitude of irrational numbers
- Arithmetic mean and geometric mean inequality
- Arithmetic mean and geometric mean inequality - Geometric interpretations
- Harmonic mean
- Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b), and sqrt(c)
- Solving inequalities for high degree polynomials factored into a product of linear binomials
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
- Solving inequalities for rational functions with non-zero right side
- Another way solving inequalities for rational functions with non-zero right side
- Advanced problems on inequalities
- Challenging problems on inequalities
- Solving systems of inequalities in two unknowns graphically in a coordinate plane
- Solving word problems on inequalities
- Proving inequalities
- Math circle level problem on inequalities
- Math Olympiad level problems on inequalities
- Entertainment problems on inequalities
under the topic Inequalities, trichotomy of the section Algebra-I.
My lessons on domains of functions are
- Domain of a function which is a quadratic polynomial under the square root operator
- Domain of a function which is a high degree polynomial under the square root operator
- Domain of a function which is the square root of a rational function.
under the topic Functions, Domain of the section Algebra-I.
See also OVERVIEW of lessons on inequalities and domains of functions.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 3003 times.
|
| |
