|
This Lesson (Solving inequalities for rational functions with non-zero right side) was created by by ikleyn(52750)   : View Source, ShowAbout ikleyn:
Solving inequalities for rational functions with non-zero right side
In this lesson you will learn how to solve inequalities for rational functions with non-zero right side. We will consider the following typical examples:
1)  < <  ; 2) ; 2)  < <  ; 3) ; 3)  > >  ; 4) ; 4)  > >  . .
Problem 1Solve an inequality  < < 
Solution
 < 2. (1)
1. Assume that x - 6 > 0, i.e. x > 6.
Multiply both sides of (1) by (x-6), which is positive in this case. You will get an inequality
x < 2*(x-6) ---> x < 2x - 12 ---> 12 > x.
Thus he solution in this case is the set of real numbers {x | 6 < x < 12}, i.e the interval (6,12).
2. Assume that x - 6 < 0, i.e. x < 6.
Multiply both sides of (1) by (x-6), which is negative in this case. You will get an inequality
x > 2*(x-6) ---> x > 2x - 12 ---> 12 > x.
(Notice that I changed the inequality sign when multiplied by negative number!)
Thus the solution in this case is the set of real {x | x < 6}, i.e the semi-infinite interval ( < 2. (1)
1. Assume that x - 6 > 0, i.e. x > 6.
Multiply both sides of (1) by (x-6), which is positive in this case. You will get an inequality
x < 2*(x-6) ---> x < 2x - 12 ---> 12 > x.
Thus he solution in this case is the set of real numbers {x | 6 < x < 12}, i.e the interval (6,12).
2. Assume that x - 6 < 0, i.e. x < 6.
Multiply both sides of (1) by (x-6), which is negative in this case. You will get an inequality
x > 2*(x-6) ---> x > 2x - 12 ---> 12 > x.
(Notice that I changed the inequality sign when multiplied by negative number!)
Thus the solution in this case is the set of real {x | x < 6}, i.e the semi-infinite interval ( , , ).
Answer. The solution is the union of two intervals: ( ).
Answer. The solution is the union of two intervals: ( , , ) U ( ) U ( , , ).
The plot of the function f(x) = ).
The plot of the function f(x) =  is shown in Figure 1. is shown in Figure 1.
|
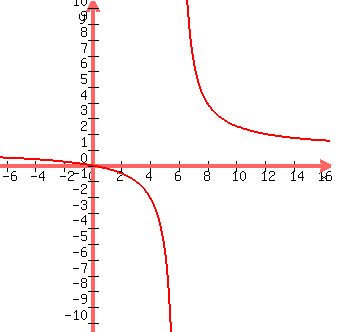 Figure 1. Plot y =
Figure 1. Plot y = 
|
Problem 2Solve an inequality  < <  . .
Solution
 < 3. (2)
1. Assume that x > 0.
Multiply both sides of (2) by 3x, which is positive in this case. You will get an inequality
x - 5 < 9x ---> -5 < 8x ---> x > < 3. (2)
1. Assume that x > 0.
Multiply both sides of (2) by 3x, which is positive in this case. You will get an inequality
x - 5 < 9x ---> -5 < 8x ---> x > 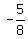 .
Thus he solution in this case is the set of real numbers {x | x > 0}, i.e the interval ( .
Thus he solution in this case is the set of real numbers {x | x > 0}, i.e the interval ( , , ).
2. Assume that x < 0.
Multiply both sides of (2) by 3x, which is negative in this case. You will get an inequality
x -5 > 9x ---> -5 > 8x ---> x < ).
2. Assume that x < 0.
Multiply both sides of (2) by 3x, which is negative in this case. You will get an inequality
x -5 > 9x ---> -5 > 8x ---> x < 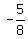 .
(Notice that I changed the inequality sign when multiplied by negative number!)
Thus the solution in this case is the set of real {x | x < .
(Notice that I changed the inequality sign when multiplied by negative number!)
Thus the solution in this case is the set of real {x | x < 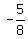 }, i.e the semi-infinite interval ( }, i.e the semi-infinite interval ( , ,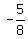 ).
Answer. The solution is the union of two intervals: ( ).
Answer. The solution is the union of two intervals: ( , ,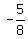 ) U ( ) U ( , , ).
The plot of the function f(x) = ).
The plot of the function f(x) =  is shown in Figure 2. is shown in Figure 2.
|
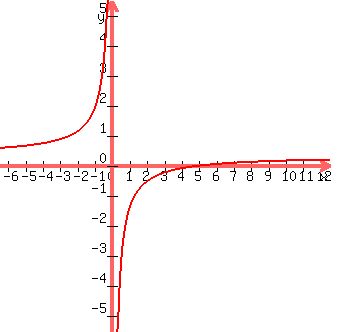 Figure 2. Plot y =
Figure 2. Plot y = 
|
Problem 3Solve an inequality  > >  . .
Solution
 > 4. (3)
1. First, let us assume that x+1 > 0.
In other words, we will consider now real numbers { x | x > -1 }.
Multiply both side of (1) by (x+1), which is positive in this case. Then you will get inequality
3x+2 > 4*(x+1) ---> 3x+2 > 4x+4 ---> 2-4 > 4x-3x ---> -2 > x.
Thus we obtain this: if x > -1, then x < -2.
It is, surely, absurd.
So, in the domain x > -1 there is no solution to (1).
2. Next, let us consider the interval x < -1. In this interval, the denominator (x+1) is negative.
Multiply both side of (3) by (x+1), which is negative now. Then you will get
3x+2 < 4*(x+1). (4)
Notice that I changed the sign ">" of the inequality to the opposite sign "<", when
multiplied both sides of (1) by negative number (x+1).
Further, (2) implies 3x+2 < 4x+4 ---> 2-4 < 4x-3x ---> -2 < x, or x > -2.
Thus we obtain this: if x < -1, then x > -2.
It means that the set of real numbers -2 < x < -1 satisfies the inequality (3).
It is the solution of the inequality (3).
Answer. The solution to (3) is the interval (-2,-1).
The plot of the function > 4. (3)
1. First, let us assume that x+1 > 0.
In other words, we will consider now real numbers { x | x > -1 }.
Multiply both side of (1) by (x+1), which is positive in this case. Then you will get inequality
3x+2 > 4*(x+1) ---> 3x+2 > 4x+4 ---> 2-4 > 4x-3x ---> -2 > x.
Thus we obtain this: if x > -1, then x < -2.
It is, surely, absurd.
So, in the domain x > -1 there is no solution to (1).
2. Next, let us consider the interval x < -1. In this interval, the denominator (x+1) is negative.
Multiply both side of (3) by (x+1), which is negative now. Then you will get
3x+2 < 4*(x+1). (4)
Notice that I changed the sign ">" of the inequality to the opposite sign "<", when
multiplied both sides of (1) by negative number (x+1).
Further, (2) implies 3x+2 < 4x+4 ---> 2-4 < 4x-3x ---> -2 < x, or x > -2.
Thus we obtain this: if x < -1, then x > -2.
It means that the set of real numbers -2 < x < -1 satisfies the inequality (3).
It is the solution of the inequality (3).
Answer. The solution to (3) is the interval (-2,-1).
The plot of the function  is shown in Figure 3. is shown in Figure 3.
|
 Figure 3. Plot y =
Figure 3. Plot y = 
|
Problem 4Solve an inequality  > >  . .
Solution
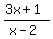 > 2. (5)
1. First, let us assume that x-2 > 0.
In other words, we will look now for solutions in the domain { x | x > 2 }.
Multiply both side of (5) by (x-2), which is positive in this case. Then you will get inequality
3x+1 > 2*(x-2) ---> 3x+1 > 2x-4 ---> 3x - 2x > -4 -1 ---> x > -5.
Thus we obtain this: the solution is the intersection of two sets: {x| x > 2} and {x| x > -5}.
This intersection is the set {x| x > 2}.
So, the interval ( > 2. (5)
1. First, let us assume that x-2 > 0.
In other words, we will look now for solutions in the domain { x | x > 2 }.
Multiply both side of (5) by (x-2), which is positive in this case. Then you will get inequality
3x+1 > 2*(x-2) ---> 3x+1 > 2x-4 ---> 3x - 2x > -4 -1 ---> x > -5.
Thus we obtain this: the solution is the intersection of two sets: {x| x > 2} and {x| x > -5}.
This intersection is the set {x| x > 2}.
So, the interval ( , , ) is the solution to (5), under the assumption that x > 2.
2. Next, let us consider the domain x < 2. In this domain, the denominator (x-2) is negative.
Multiply both side of (1) by (x-2), which is negative now. Then you will get
3x+1 < 2*(x-2). (6)
Notice that I changed the sign ">" of the original inequality to the opposite sign "<", when
multiplied both sides of (5) by negative number (x-2).
Now, (6) implies 3x+1 < 2x-4 ---> 3x - 2x < -4 -1 ---> x < -5.
Thus by analyzing the domain x < 2 we obtain the solution x < -5.
By collecting the results of n.1 and n.2 you get the full solution set.
It is the union ( ) is the solution to (5), under the assumption that x > 2.
2. Next, let us consider the domain x < 2. In this domain, the denominator (x-2) is negative.
Multiply both side of (1) by (x-2), which is negative now. Then you will get
3x+1 < 2*(x-2). (6)
Notice that I changed the sign ">" of the original inequality to the opposite sign "<", when
multiplied both sides of (5) by negative number (x-2).
Now, (6) implies 3x+1 < 2x-4 ---> 3x - 2x < -4 -1 ---> x < -5.
Thus by analyzing the domain x < 2 we obtain the solution x < -5.
By collecting the results of n.1 and n.2 you get the full solution set.
It is the union ( , , ) U ( ) U ( , , ).
The problem is solved.
Answer. The solution to (5) is the union ( ).
The problem is solved.
Answer. The solution to (5) is the union ( , , ) U ( ) U ( , , ).
The plot of the function ).
The plot of the function  is shown in Figure 4. is shown in Figure 4.
|
 Figure 4. Plot y =
Figure 4. Plot y = 
|
My other lessons on solving inequalities are
- Solving simple and simplest linear inequalities
- Solving absolute value inequalities
- Advanced problems on solving absolute value inequalities
- Solving systems of linear inequalities in one unknown
- Solving compound inequalities
- What number is greater? Comparing magnitude of irrational numbers
- Arithmetic mean and geometric mean inequality
- Arithmetic mean and geometric mean inequality - Geometric interpretations
- Harmonic mean
- Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b), and sqrt(c)
- Solving problems on quadratic inequalities
- Solving inequalities for high degree polynomials factored into a product of linear binomials
- Solving inequalities for rational functions with numerator and denominator factored into a product of linear binomials
- Another way solving inequalities for rational functions with non-zero right side
- Advanced problems on inequalities
- Challenging problems on inequalities
- Solving systems of inequalities in two unknowns graphically in a coordinate plane
- Solving word problems on inequalities
- Proving inequalities
- Math circle level problem on inequalities
- Math Olympiad level problems on inequalities
- Entertainment problems on inequalities
under the topic Inequalities, trichotomy of the section Algebra-I.
My lessons on domains of functions are
- Domain of a function which is a quadratic polynomial under the square root operator
- Domain of a function which is a high degree polynomial under the square root operator
- Domain of a function which is the square root of a rational function.
under the topic Functions, Domain of the section Algebra-I.
See also OVERVIEW of lessons on inequalities and domains of functions.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 2166 times.
|
| |

