|
Question 207043This question is from textbook Elementary and intermediate algebra
: I am asked to solve the following inequalities and state the solution set using the interval. I am totally lost. Would you please explain to me how to solve these two inequalities step by step so I can understand how they work. Thank you!!
a. 3x-x^2>0
b. (x+3)/x<=2
This question is from textbook Elementary and intermediate algebra
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Solving quadratic inequalities is similar to solving quadratic equations. Get one side equal to zero and factor:
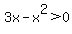
One side is already 0 so we just factor. (GCF first, always):
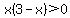
Now we have a product which is less than zero. In other words we have a product which is negative. How can we get a negative result when multiplying two numbers? Answer: One number has be be negative and the other has to be positive.
Now we can solve the inequality using this fact. We simply state mathematically the idea that either (x) is positive and (3-x) is negative or (x) is negative and (3-x) is positive:
( and  ) or ( and  )
Now we solve these for x. We just have to add x to both sides of the 2nd and 4th inequalities:
( and  ) or ( and  )
It helps to read inequalities from where the variable is. In the 2nd and 4th inequalities the variable is on the right. So we should read them from right to left! The 2nd one says: "x is greater than 3". The 4th one says "x is less than 3". (Look at these and see if you can learn how to read these right-to-left inequalities.)
Now lets look at the first pair:
( and )
One says "x is greater than 0" and the other says "x is greater than 3". With an "and" between them both must be true. With some thought (and perhaps with number line graphs to help) we should be able to fiugure out that if  then both inequalities will be true. So the first pair simplfies to: .
Using similar logic on the second pair:
( and )
One says "x is less than 0" and the other says "x is less than 3". With an "and" between them both must be true. With some thought (and perhaps with number line graphs to help) we should be able to figure out that if then both inequalities will be true. So the first pair simplfies to: .
Now we have:
or
In interval notation this would be:
( , 0) or (3,  )
The second problem requires an understanding of how to solve the related equation:  and how the steps to solving it work with inequalities. The first step for solving the equation (and the inequality) is to multiply both sides by (x) to eliminate the fraction. So we multiply both sides by (x) and get (x+3) on the left and 2x on the right. We just have to figure out what the inequality symbol should be after this multiplication.
With equations we can multiply both sides by any non-zero number and not worry about it. But with inequalities we must be concerned about whether the number we are multiplying by is positive or negative. If it is negative then we must reverse the inequality.
But we are muliplying by (x) and we don't know what (x) is!? So we have to take into account both possibilities:- x is positive so we do not reverse the inequality
- x is negative and we must reverse the inequality
We simply state the above mathematically:
( and  ) or ( and  )
Now we solve. Just subtract x from both sides of the 2nd and 4th inequalities:
( and  ) or ( and  )
Like problem 1 we will read the inequalities from where the variable is and analyze each pair. The first pair:
( and )
They say "x is greater than 0" and "x is greater than or equal to 3". With the "and" between them they both must be true. Only if  will both be true.
The second pair:
( and )
They say "x is less than 0" and "x is less than or equal to 3". Only if will both be true.
So the solution simplifies to:
 or
In interval notation this would be:
(, 0) or [3, ).
Note the "[" on the second interval. It means that the number on that end, the 3, is part of the solution set. The parentheses elsewhere mean that the numbers, (0, infinity, -infinity) are not part of the solution.
|
|
|
| |
