Question 145950: Bayside Insurance offers two health plans. Under plan A, Giselle would have to pay the first $50 of her medical bills, plus 25% of the rest. Under plan B, Giselle would pay the first $230, but only 20% of the rest. For what amount of medical bills will plan B save Giselle money? Assume she has over $230 in bills.
Suppose Giselle has a certain amount in medical bills, such as $5000. How much would she pay under each plan?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! "For what amount of medical bills will plan B save Giselle money?"
Let x=amount of the bill
Under plan A, the expression is

Under plan B, the expression is

So to figure out when plan B will save her money, simply set the plan B expression less than the plan A expression


 Distribute Distribute
 Combine like terms Combine like terms
 Subtract 0.25x from both sides. Subtract 184 from both sides. Subtract 0.25x from both sides. Subtract 184 from both sides.
 Combine like terms Combine like terms
 Divide both sides by 0.45 Divide both sides by 0.45
So if she has any bills over $2,930, then Plan B will cost less than Plan A.
-----------------------
"Suppose Giselle has a certain amount in medical bills, such as $5000. How much would she pay under each plan?"
 Start with the Plan A expression Start with the Plan A expression
 Plug in Plug in 
 Subtract Subtract  from from 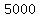 to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Add Add  and and  to get to get  . .
So under Plan A, she will pay $1,287.50
----------------------
 Start with the Plan B expression Start with the Plan B expression
 Plug in Plug in 
 Subtract Subtract  from from 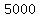 to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Add Add  and and  to get to get  . .
So under Plan B, she will pay $1,184.00
|
|
|