Question 135881: Please help me solve this equation: (x-1)/(x+2) > 0
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! First let's get your terminology correct.  is NOT an equation, it is an inequality.
You have already completed step 1 for solving rational inequalities, and that is to arrange the inequality so that you have 0 on one side (generally the right) and everything else on the other side.
Step 2: Find the boundary points:
Step 2A: Set the numerator equal to zero and solve:  => 
Step 2B: Set the denominator equal to zero and solve:  => 
Step 3: Determine whether your solution will be inclusive or exclusive of the boundary points.
Step 3A: , since the entire fraction must be larger and not equal to zero, the boundary point must be excluded from the solution set because if the numerator is equal to zero so the entire fraction would be zero.
Step 3B: , since a denominator can never be zero, -2 must be excluded from the solution set.
Step 4: Now you have defined three intervals: ( , ), (, ), and (, )
Step 5: Select any convenient value from the first interval, -3 will do. Substitute this value into the original inequality:
 Since the result is positive, values in this interval are included in the solution set of the inequality. A positive result means the interval is included because the original inequality has the rational expression greater than zero, or positive.
Step 6 and 7: Repeat step 5 for the other two intervals:
Select 0 from the second interval:
 Since the result is negative, values in this interval are excluded.
Select 2 from the third interval:
 Again, since the result is positive, values in this interval are included in the solution set of the inequality.
Therefore your solution set is all real x such that  or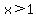 
|
|
|
