abs(x) = x if x is positive and equals -x if x is negative.
x represents any expression that is included as an argument in the absolute value function.
therefore:
abs(x-2) < 4 becomes:
(x-2) < 4 if (x-2) is positive, .....
and -(x-2) < 4 if (x-2) is negative.
when (x-2) is positive, you would solve for x as follows:
x-2 < 4
add 2 to both sides of the inequality to get:
x < 6
when (x-2) is negative, you would solve for x as follows:
-(x-2) < 4
simplify to get:
-x + 2 < 4
subtract 2 from both sides to get:
-x < 2
multiply both sides by -1 to get:
x > -2
don't forget that multiplying both sides of an inequality by the same negative number reverses the inequality.
so your answer is:
x < 6 or x > -2
this can be written as -2 < x < 6
abs(x-2) < 4 when x is greater than 2 and when x is < 6
to test this out, let x equal values that satisfy the solution and that do not satisfy that solution.
any value of x > -2 and < 6 will satisfy the solution.
i choose 4
when x = 4, abs(x-2) < 4 becomes abs(4-2) < 4 which becomes abs(2) < 4 which becomes 2 < 4 which is true.
i choose x = -3 and x = 7 as values which do not satisfy the solution range.
when x = -3, abs(x-2) < 4 becomes abs(-3-2) < 4 which becomes abs(-5) < 4 which becomes 5 < 4 which is false.
when x = 7, abs(x-2) < 4 becomes abs(7-2) < 4 which becomes abs(5) < 4 which becomes 5 < 4 which is false.
you can also graph the equation of y = abs(x) and y = 4 and it will show you graphically when the equation of y = abs(x) is smaller than 4.
that graph is shown below:
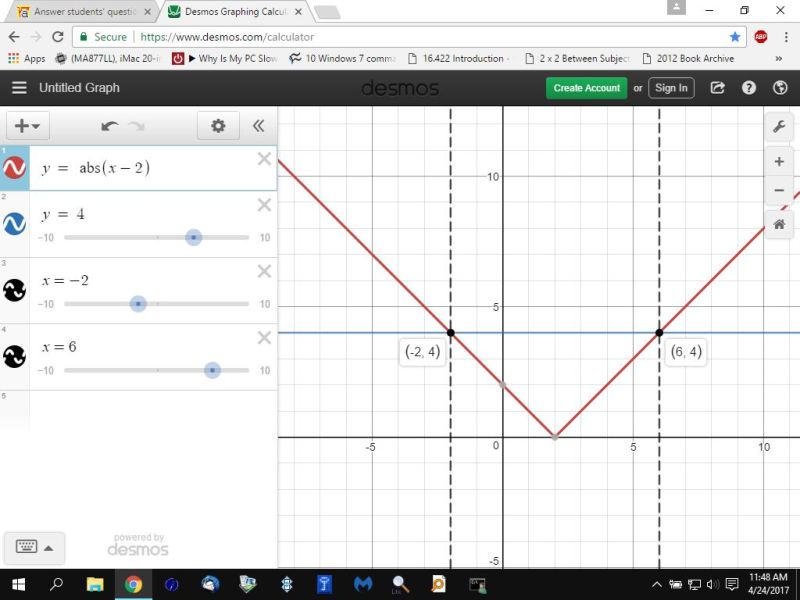
from the graph, you can see that the value of y = abs(x-2) is less than the value of y = 4 when x is greater than -2 through x is smaller than 6 only.
the coordinate points are shown in the format of (x,y), where x represents the value of the x-coordinate and y represents the value of the y coordinate.
for example, when x = -2, then the value of y = abs(x-2) becomes y = abs(-2-2) which becomes y = abs(-4) which becomes y = 4, which provides you with the coordinate point of (-2,4).