SOLUTION: If f(x)= 2x^3-x^2+3x+10 and g(x)= x^3+3x^2+2x+4, determine when f(x)>g(x) using a factor table strategy.

I don't know about "factor table strategy", but
here is the way I'd go about solving the problem:





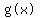
Get 0 on the right:



We find the critical values, which are the zeros of 

Use synthetic division, trying the factors of 6, which are ±1,±2,±3,±6 

1 | 1 -4  1  6
  |    1 -3 -2
    1 -3 -2  4

Remainder isn't 0.  Try -1

-1 | 1 -4  1  6
   |   -1  5 -6
     1 -5  6  0

So  factors as

(x+1)(x2-5x+6) 

and it factors completely as

(x+1)(x-2)(x-3) > 0

So the critical numbers are -1,2, and 3

Intervals to test (between and beyond those):

1.  

Test x=-2, (-2+1)(-2-2)(-2-3) > 0
                 (-1)(-4)(-5) > 0
                          -20 > 0
FALSE!

2.  

Test 0, (0+1)(0-2)(0-3) > 0
            (1)(-2)(-3) > 0
                      6 > 0
TRUE!

3. 

Test 2.5, (2.5+1)(2.5-2)(2.5-3) > 0
               (3.5)(0.5)(-0.5) > 0
                         -0.875 > 0
FALSE!



Test 4, (4+1)(4-2)(4-3) > 0
              (5)(2)(1) > 0
                     10 > 0
TRUE!

So f(x) > g(x) when  -1 < x < 2, and when x > 3

Edwin