SOLUTION: 2.a On an oblique triangle A=625 ft.C=189ft.,B=102.0 degrees

Every triangle has six parts, three angles and three sides.

If you know three of these parts, you can usually find the other
three parts by calculating.

But you must be careful with the capital and small letters
A, B, C, a, b, and c.  Capital and small letters are NOT 
interchangeable.  

The capital letters A, B, C, refer to the three angles only.
The small letters a, b, c, refer to the three sides only.
Side a is across the triangle from angle A.
Side b is across the triangle from angle B.
Side c is across the triangle from angle C.

Here is a picture of your triangle:



This is the case SAS, where the given angle is
between two given sides.

In this case we first use the law of cosines to find
the third (unknown) side, b.

b² = a² + c² - 2ab·cos(B)
b² = 625² + 189² - 2(625)(189)·cos(102.0°)
b² = 625² + 189² - 2(625)(189)(-.2079116908)
b² = 390625 + 35721 + 49199.13696
b² = 475465.137
     __________
b = Ö475465.137  

b = 689.5398008 feet

You should round that to 690 feet in the final
answer, but you must keep all those decimals
when you use b to calculate one of the unknown
angles.

To find either unknown angle, we use the law
of sines:

 =  = 

To find angle A, we use only the first two parts

 = 

Solve for sin(A) by first cross multiplying

 = 

Then we divide both sides by 

 = 

Substituting, using all the decimals in b,
not the rounded off version.

 = 

 = 

Now we find the inverse sine of that, and get

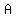 = 62.44839410°

We round that off to tenths of a degree, 62.4°
in the final answer because that's the way the 
given angle was rounded.

Now all we have to do to find angle C is to
use the fact that the three angles of any
triangle must have sum 180°.

A + B + C = 180°

62.44839410° + 102.0° + C = 180°

164.4483942° + C = 180°
               C = 180°- 164.4483942°
               C = 15.55160581°
               C = 15.6°

So the three missing parts of the
triangle are:

A = 62.4°
b = 690 ft.
C = 15.6°

-------------------------------

Now as a check, let's see if we get the same thing
for angle C if we use the law of sines as we did to
find angle A:

we use the law
of sines:

 =  = 

To find angle C, we use only the last two parts

 = 

Solve for sin(C) by first cross multiplying

 = 

Then we divide both sides by 

 = 

Substituting, again using all the decimals in b,
not the rounded off version.

 = 


 = 

Now we find the inverse sine of that, and get

 = 15.55160581°

That is exactly what we got when we found angle
C the other way.  So we know we are correct.

Edwin