Question 979372: without graphing, determine whether each equation has a graph that is symmetric with respect to the x-axis, the origin, or none of these.
a. Y=2x4-3(Note:the x is to the 4th power, I don't know how to write it on here.)
b. y=x+15
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
a. 
We can often see symmetry visually, but to be really sure we should check a simple fact:
For symmetry with respect to the y-axis, check to see if the equation is the same when we replace  with with  : :
is  symmetric about the y-axis? symmetric about the y-axis?
Try to replace  with with  : :

Since  (multiplying a negative times a negative gives a positive), there is (multiplying a negative times a negative gives a positive), there is  change. change.
So,  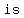 symmetric about the y-axis symmetric about the y-axis
For symmetry about x-axis use the same idea as for the y-axis, but try replacing  with with 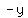 . .



Now try to get the original equation:
 => It is => It is 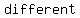 . .
Hence  is is  symmetric about the x-axis symmetric about the x-axis
Diagonal symmetry:
Try swapping  and and  : :

rearrange :



And we do not have the original equation. They are not the same.
Hence  has has  diagonal symmetry. diagonal symmetry.
Origin symmetry is when every part has a matching part:
the same distance from the central point
but in the opposite direction.
Check to see if the equation is the same when we replace both  with with  and and  with with 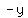 . .
does  have origin symmetry? have origin symmetry?
Start with:

Replace  with with  and and  with with 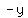 : :


the left side is 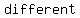 from the original equation and the right side is identical to the original equation, and this isnít equivalent to the original equation and we do from the original equation and the right side is identical to the original equation, and this isnít equivalent to the original equation and we do  have symmetry about the origin have symmetry about the origin
so,  is is  symmetric about the origin symmetric about the origin
b.

to check is it symmetric about the y-axis, replace  with with  : :
 => is different from the original equation, so it is not symmetric about the y-axis => is different from the original equation, so it is not symmetric about the y-axis
to check is it symmetric about the x-axis, replace  with with 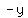 : :
 => is different from the original equation, so it is not symmetric about the x-axis => is different from the original equation, so it is not symmetric about the x-axis
To test for symmetry over the origin, you replace  with with  , and , and  with with . .
Again if the equation is identical to the original equation, then the graph is symmetric over the origin.
 => the equation is not identical to the original equation, so it is not symmetric over the origin => the equation is not identical to the original equation, so it is not symmetric over the origin
remember: The linear equations  or or  are the only two equations which are symmetric over the origin. are the only two equations which are symmetric over the origin.
Note that most graphs donít have any kind of symmetry. Also, it is possible for a graph to have more than one kind of symmetry. For example the graph of a circle centered at the origin exhibits all three symmetries.
|
|
|