|
Question 249011: Graph the function. State domain, range, y intercept.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!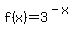 
Domain.
When determining the domain of a function you start by assuming that the domain is all Real numbers. Then you figure out if there are numbers which should be excluded. Numbers to exclude are those that:- make any denominator zero.
- make the radicand of an even-numbered root negative. For example, for
 we would have to exclude all numbers less than -3 because they would make the radicand (this number inside) of the square root negative. (Square roots are 2nd roots so they count as one of the even-numbered roots.) - the argument to any logarithm zero or negative.
- would create any other "no-no" (like
 ).
f(x) has no denominators, no logarithms and no even-numbered roots. The x is in the exponent of a 3. There aren't any no-no's for exponents. Exponents can be any number. So x can be any number. The domain is all Real numbers.
Range.
Since the range is the set of function outputs and since the outputs of a function are determined by its inputs, we need to know the domain first in order to find the range. We have already done this and the domain is all Real numbers. Next we analyze the function and try to find all the possible outputs that can result for all the different x values in the domain. There are a couple of ways to do this:- Use your understanding of how "things" work. For this function we need to understand how exponents work. When x can be any number, what are the possible results for
 ? If we do understand exponents we would know that there is no way to raise 3 to some power and get zero. Nor is it possible to raise 3 to some power and get a negative. (Remember that negative exponents mean "reciprocal", not negative. For example  .) We can achieve any positive number by raising 3 to an appropriate power. We can get numbers between 0 and 1 by using neagtive exponents, we can get 1 by using a 0 for the exponent and we can get any number above one by using positive exponents. So the range is all positive numbers. - Use the inverse. Since the inverse of a function is the function with its x's and y's swapped, the range of the function is the domain of the inverse (and vice versa). So let's find the inverse and then find its domain:
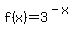
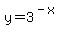
Swap the x's and y's:
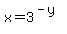
Solve for y (by finding the base 3 logarithm of each side):
Use the property of logarithms,  , to move the exponent of the argument in front of the logarithm on the right side of the equation:
Since  by definition we get:
Multiply both sides by -1:
This is the inverse of f(x). What is its domain? Well we have a logarithm and we cannot allow the argument of a logarithm to be zero or negative. So the domain is all positive numbers. And since the domain of the function's inverse is all positive numbers, then the range of the function is all positive numbers.
As you can see, either way we get a range of all positive numbers.
Y-intercept.
This is the easy part. Since the x coordinate is zero for all points on the y-axis, the y-intercept is found by using zero for the x value:
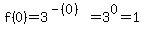
The Y-intercept is 1.
Here's the graph. (It does not ever touch the x-axis, even for extremely large values of x. If it looks like it does, then it is flaw in the Algebra.com's graphing facility.)
|
|
|
| |
