SOLUTION: Solve. Use a graphing calculator if necessary. See Examples 9-11. (Objective 8) The cost C in dollars of operating a certain concrete-cutting machine is related to the number of

Question 1169985: Solve. Use a graphing calculator if necessary. See Examples 9-11. (Objective 8)
The cost C in dollars of operating a certain concrete-cutting machine is related to the number of minutes n the machine is run by the function
C(n) = 1.2n2 − 24n + 690.
For what number of minutes is the cost of running the machine a minimum? What is the minimum cost?
Question: The minimum cost is $ ?for
minutes?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
this is a quadratic equation.
replace n with x to get:
c(x) = 1.2x^2 - 24x + 690
this is in standard form where:
a = coefficient of x^2 term = 1.2
b = coefficient of x term = -24
c = constant term = 690
the minimum point of this equation will be when x = -b/(2a)
that becomes when x = -(-24)/(2*1.2) = 24/2.4 = 10
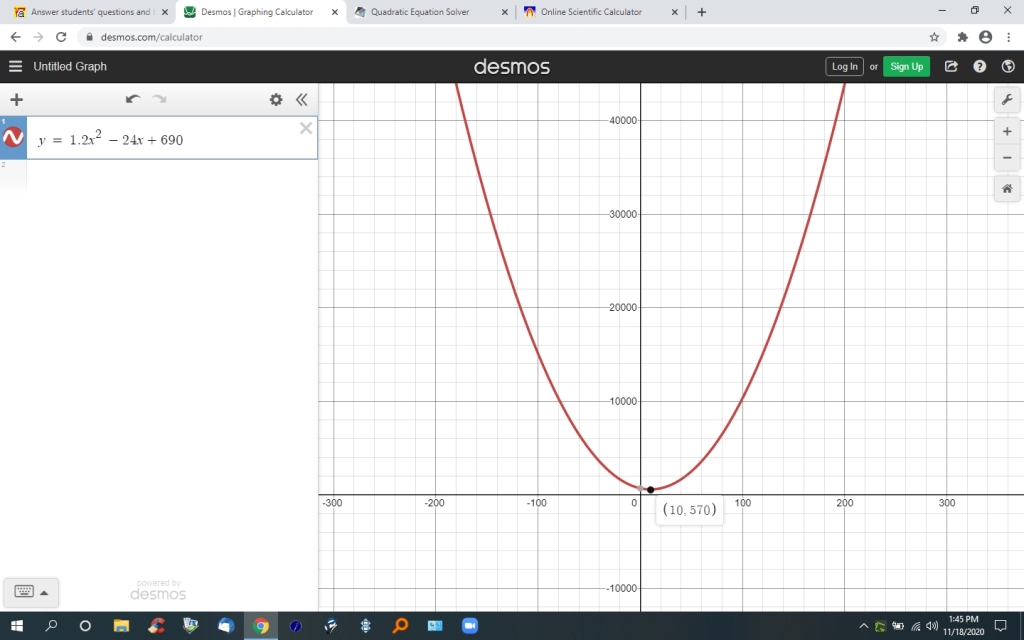
when x = 10, 1.2x^2 - 24x + 690 = 1.2*10^2 - 24*10 + 690 = 570.
the minimum point of the equation will be at the point (x,y) = (10,570).

here's the graph.

RELATED QUESTIONS
Solve. Use a graphing calculator if necessary. See Examples 9 - 11. (Objective 8) The... (answered by Boreal)

Use a calculator to solve the application. See Examples 9-10. (Objective 6) Find the... (answered by ikleyn)

Use a calculator to solve the application. See Examples 9-10. (Objective 6) Find the... (answered by mananth)

Solve. Use a graphing calculator if necessary. See Examples 9 - 11. (Objective 8) From (answered by ikleyn)

The cost c(in dollars) of operating a certain concrete-cutting machine is related to the... (answered by jim_thompson5910)

Operating Cost: A delivery company has a fleet of vans. The annual operating cost C (in... (answered by Cromlix)

Use two equations in two variables to solve the application. See Example 1. (Objective 1) (answered by ikleyn)

Use two equations in two variables to solve the application. See Example 1. (Objective 1) (answered by Boreal)