start with kx^2 - 2kx - x^2 + 2x + k - 1 = f(x)
set f(x) = 0 and rearrange the terms with like terms next to each other and in descending order of degree to get:
kx^2 - 2kx + k - x^2 + 2x - 1 = 0
group the terms as shown below:
(kx^2 - 2kx + k) - (x^2 - 2x + 1) = 0
factor out the k in the left goruping to get:
k * (x^2 - 2x + 1) - (x^2 - 2x + 1) = 0
factor out the (x^2 - 2x + 1) to get:
(x^2 - 2x + 1) * (k - 1) = 0
divide both sides of the equation by k-1 to get:
(x^2 - 2x + 1) = 0 / (k - 1)
factor the left side of the equation to get:
(x - 1)^2 = 0 / (k - 1)
the right side of the equation will be equal to 0 for all values of k except 1.
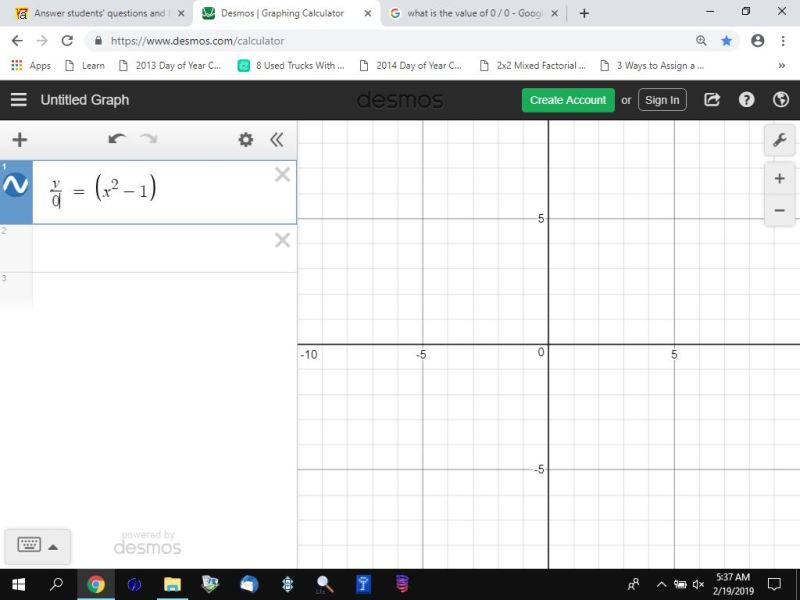
the equation is undefined when k = 1 because 0 / 0 is undefined.
for all values of k except 1, the equation becomes (x-1)^2 = 0 because 0 divided by anything except 0 is equal to 0.
take the square root of both sides of the equation to get plus or minus (x-1) = 0
this makes x = plus or minus 1.
the roots of the equation will be x = plus or minus 1 for all values of k except k = 1.
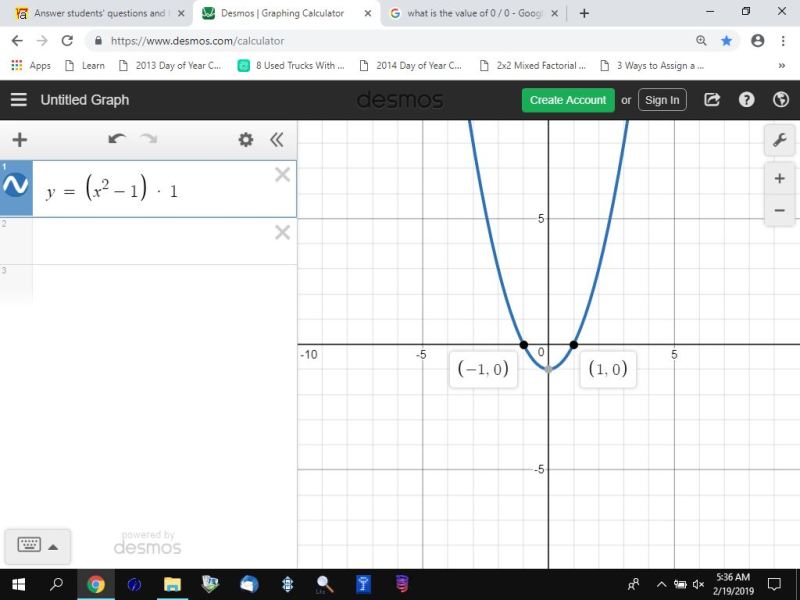
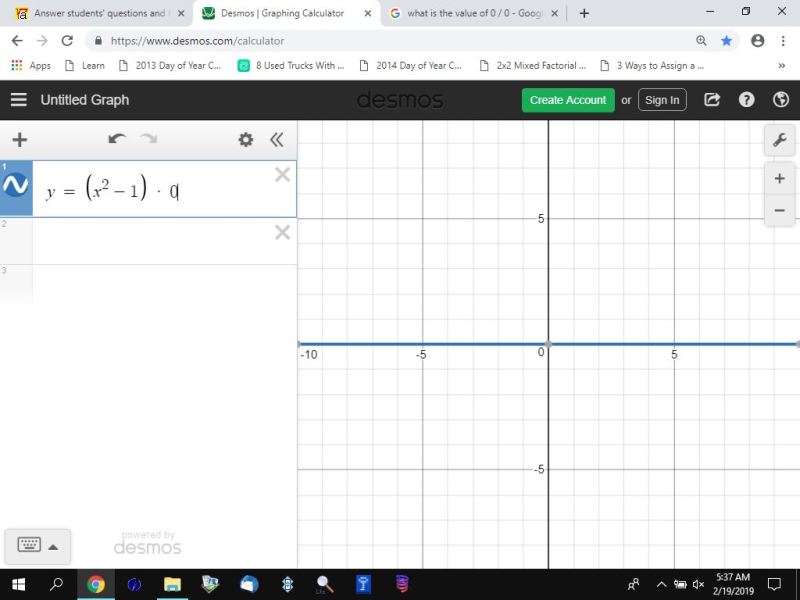
if you graph the equation of y = (x-1)^2 * (k-1) for different values of k, then you will get a quadratic equation except for k = 1 where you will get a horizontal line at y = 0.
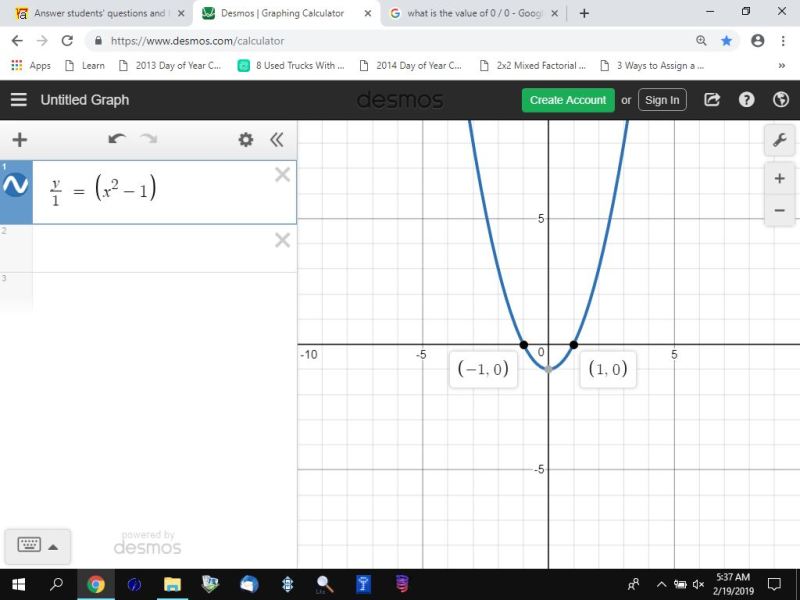
if you divide both sides of the equation by (k-1), you will graph y/(k-1) = (x-1)^2 and get a graph of a quadratic equation for all values of k except 1 and you will not get a graph at all for k = 1 because the software doesn't know what to do with y/0 since it is undefined.
here's a couple of graphs of y = (x-1)^2 * (k-1) for k = 2 and k = 1 followed by a couple of graphs of y/(k-1) = (x-1)^2 for k = 2 and k = 1.
when k = 1, (k-1) = 1
when k = 1, (k-1) = 0