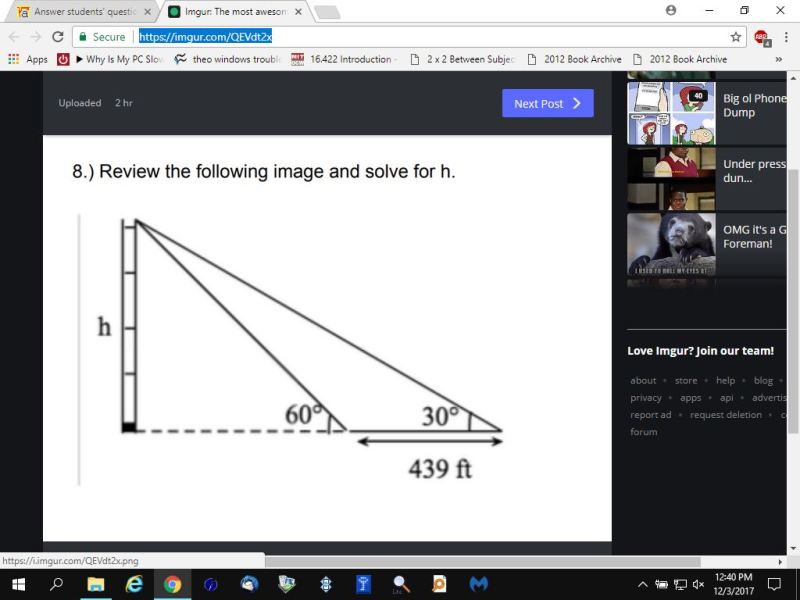
assign x to the value of the length of the dashed line.
you get:
tan(60) = h/x
tan(30) = h/(x+439)
solve for h in both equations.
you get h = tan(60) * x
you get h = tan(30) * (x + 439)
since they both equal to h, then they are both equal to each other and you get:
tan(60) * x = tan(30) * (x + 439)
simplify to get tan(60) * x = tan(30) * x + tan(30) * 439
subtract tan(30) * x from both sides of the equation to get tan(60) * x - tan(30) * x = tan(30) * 439
factor out the x to get (tan(60) - tan(30)) * x = tan(30) * 439
divide both sides of this equation by (tan(60) - tan(30)) to get x = (tan(30) * 439) / (tan(60) - tan(30))
simplify to get x = 219.5
h = x * tan(60) becomes h = 219.5 * tan(60) which becomes h = 380.1851523.
h = (x + 439) * tan(30) becomes h = (219.5 + 439) * tan(30) which becomes h = 658.5 * tan(30) which becomes h = 380.1851523.
the formula are both in agreement that h = 380.1851523.