SOLUTION: f(x)= 2x^2-16x+30
g(x)= x*(x-3)^2*(x+1)^4
Find the zeros of g(x) and f(x).
Algebra.Com
Question 1009152: f(x)= 2x^2-16x+30
g(x)= x*(x-3)^2*(x+1)^4
Find the zeros of g(x) and f(x).
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
set f(x) equal to 0 and you get:
2x^2 - 16x + 30 = 0
factor out a 2 and you get:
2 * (x^2 - 8x + 15) = 0
factor x^2 - 8x + 15 to get:
2 * (x-3) * (x-5) = 0
set each of these factors equal to 0 to get:
x-3 = 0 and x-5 = 0
solve for x to get x = 3 and x = 5.
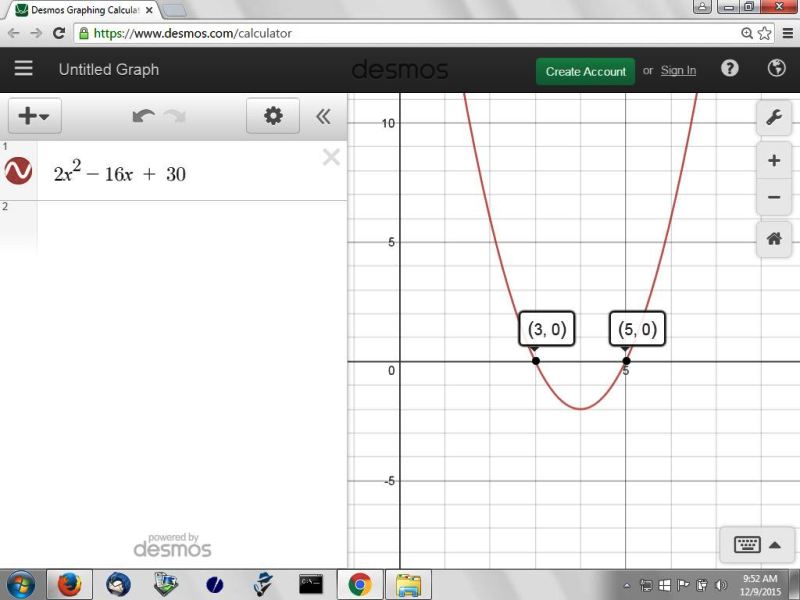
the zeroes of y = 2x^2 - 16x + 30 are at x = 3 and x = 5.
here's the graph:
your second equation is:
g(x)= x(x-3)^2 (x+1)^4
set g(x) equal to 0 and you get:
x * (x-3)^2 * (x+1)^4 = 0
set each of these factors equal to 0 and you get:
x = 0 and (x-3)^2 = 0 and (x+1)^4 = 0
solve for x in each of these equations to get:
x = 0
(x-3)^2 = 0
take square root of both sides of this equation to get:
(x-3) = 0
solve for x to get x = 3
(x+1)^4 = 0
take the fourth root of both sides of this equation to get:
x + 1 = 0
solve for x to get x = -1
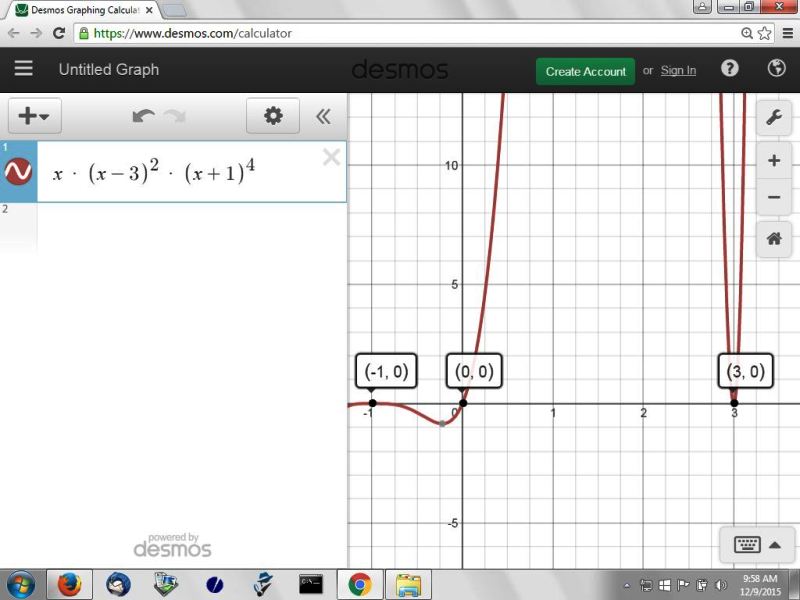
your zeroes are at x = -1, x = 0, and x = 3
here's the graph:
RELATED QUESTIONS
f(x)= 〖2x〗^2-16x+30 ,
g(x)= 〖x(x-3)〗^2... (answered by Boreal)
Given f(x)= 〖2x〗^2-16x+30 ,
g(x)= 〖x(x-3)〗^2... (answered by stanbon)
If f(x)=2x-1 and g(x)=x^2 find :
1. g(g(x))
2. g(f(x))
3. f(g(x))
4.... (answered by fcabanski)
if f(x)=2x+4 and g(x)=x^2+1, find (f o... (answered by Nate)
find (f g)(x) and (g f)(x).
f(x)=-2x^2 + 1, g(x)= -2x
(f... (answered by amarjeeth123)
Given f(x)=x/(x-1) , g(x)=(2x-4)/x find the following
a) (f•g)(0)
b) (g•f)(-2)... (answered by stanbon)
Given f(x)=2x^2-x-3 and g(x)=x+1 find... (answered by user_dude2008)
f(x)=2x-3 and g(x)=x^2+2x+4 evaluate... (answered by ewatrrr)
3. If f(x)=square root 2x^2-1 and g(x)=x^1/2, find (and simplify)
a) (f+g)(x)
b)... (answered by CPhill)

