SOLUTION: PQRS is a parallelogram with SQ=PR. Prove that PQRS is a rectangle.

Question 897802: PQRS is a parallelogram with SQ=PR. Prove that PQRS is a rectangle.
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
If it is a parallelogram, then the opposite sides are equal.
If the diagonals are also equal, then you have 4 congruent triangles.

to show you what i mean, let the parallelogram be PQRS.

you have:

PQ = SR

PS = QR

PR = SQ

you can break your parallelogram into 4 triangles.

those triangles are:

PRS and RPQ

SPQ and QRS

all these triangles are congruent by SSS as shown in the following diagram.

$$$

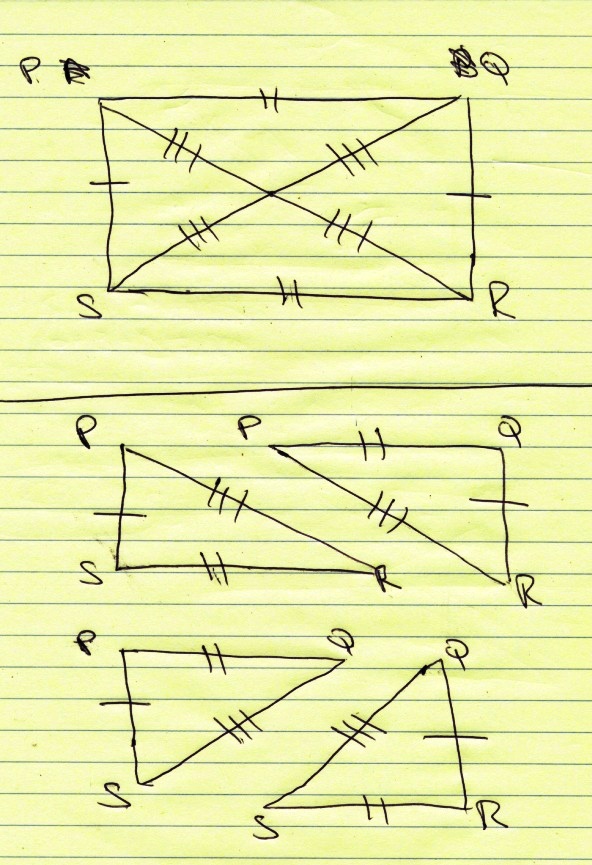
since all these triangles are congruent, then all their corresponding angles are congruent.

this means that angle PSR is congruent to angle RQP is congruent to angle SPQ is congruent to angle QRS.

this means that all 4 angles of the parallelogram are congruent to each other.

this means that all the angles of the parallelogram are equal to 90 degrees.

since all the angles of a rectangle are equal to each other, this means that the parallelogram is a rectangle.

it hss all 4 angles equal to each other.
it has both diagonals equal to each other.

that's all that you need because that's what defines a rectangle.

here's a definition of a rectangle from the web.

http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rectangle.php\

RELATED QUESTIONS
PQRS is a parallelogram with PQ=PS. Prove that RP bisects the angle QPS (answered by ikleyn)

1) ABCD is a parallelogram if AB = 2 AD and P is the midpoint of AB.prove that angle CPD... (answered by orca)

PQRS is a parallelogram. Given that OR=6 cm and SQ is 4 cm more than PR, then find the... (answered by richwmiller)

Given: Quadrilateral PQRS P= (-10,7), Q=(4,3), R=(-2,-5), S=(-16,1) a.Prove taht the... (answered by jsmallt9)

given Quadrilaterals PQRS were QR bisects PR and PR bisects QS, proves PQRS is... (answered by ikleyn)

In paralellogram PQRS, angle Q is a right angle. Is PQRS a rectangle... (answered by jim_thompson5910)

The quadrilateral PQRS has vertices P(2,4), Q(5,1), R(-1,-2) and S(-4,1). Prove that PQRS (answered by MathLover1)

if PQRS is a rectangle, PR=9x+1, and QS=13x-11, find... (answered by ikleyn)

If PQRS is a rectangle, PR=9x+1, and QS=13x-11, find... (answered by CubeyThePenguin)