|
Question 971833: Part of a cheerleading routine is throwing a flyer straight up and catching her on the way down. The flyer begins this move with her center of gravity 4 feet above the ground. She is thrown with an initial vertical velocity of 30 feet per second.
Will the flyer’s center of gravity ever reach 20 feet? In two or more complete sentences, explain how you found your answer.
For the flyer to have her center of gravity reach 25 feet, what does the initial velocity need to be? In two or more complete sentences, explain how you found your answer.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a dynamics/mechanics (physics) problem.
I do not know of a physics help website, but I can help.
Also, any cheerleader (and his/her fifth grader younger sibling)
would also be able to tell you that no team would be able to reach such ridiculous heights.
PART 1:
 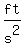 = acceleration of gravity. = acceleration of gravity.
 = time to maximum height (in seconds). = time to maximum height (in seconds).
   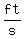 . .
During the upwards flight,   (in ft/second) decreases linearly as (in ft/second) decreases linearly as
  , ,
At the highest point of that flyer flight,
 = time to reach maximum height (in seconds). = time to reach maximum height (in seconds).
and   , so , so
so    , ,
and at that apex, the upwards velocity in ft/s is
 --> --> }--> }--> --> --> . .
Flying at an average upwards velocity of  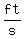 for for  seconds, seconds,
the flyer's height would increase by less than  . .
The increase in height can be calculated as   . .
With that height increase added to the initial  height, height,
the flyer's greatest attained height would be less than  , ,
and actually  . .
The height attained should be impressive enough (and scary enough).
Other calculation options including memorized complicated formulas are possible.
Two sentences:
Given the initial velocity of 20 ft/second,
the average velocity while going up would be 10ft/s,
and the time to maximum height would be less than 1 second.
Flying at an average velocity of 10 ft/second for less than 1 second,
the height would increase by less than 10 ft,
which added to the initial 4 ft height is far less than 25 ft.
PART 2 my way:
 = initial upwards velocity, in feet/second, and = initial upwards velocity, in feet/second, and
At the highest point in the flight,
the upwards velocity has gone down by  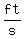 , ,
and the time to achieve that downward acceleration at a rate of  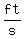 per second is per second is
 seconds. seconds.
The average velocity while flying up was  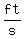 . .
to increase the flyers height by 
in  seconds at an average velocity of seconds at an average velocity of  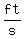 , ,
what's needed is
 <--> <--> <--> <--> <--> <-->
The complicated way:
Let's dust the formula that you are probably expected to memorize,
so you can see another way to do the calculations. It's
 , with , with
 = time in the air, in seconds, = time in the air, in seconds,
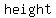 = height at = height at  seconds seconds
 = initial height, in feet = initial height, in feet
 = initial upwards velocity, in feet/second, and = initial upwards velocity, in feet/second, and
 = acceleration of gravity in = acceleration of gravity in 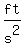 . .
Substituting the known values we get,
 . .
So 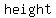 is a quadratic function of is a quadratic function of  . .
All quadratic functions (generally written as y as a function of x) can be written as
 and if and if  , ,
have a maximum at  , ,
and that maximum value is  . .
So  with with  will have a maximum for will have a maximum for
 , ,
and for that maximum to be  feet, we need feet, we need
 <--> <--> <--> <--> <--> <--> <--> <--> <--> <-->
|
|
|
| |