|
Question 1196483: Given that  and and  , find all possible values for the sum of the coefficients in the quadratic function g(x). , find all possible values for the sum of the coefficients in the quadratic function g(x).
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given that  and and  , find all possible values , find all possible values
for the sum of the coefficients in the quadratic function g(x).
~~~~~~~~~~~~~~~~~~
The key idea to solve this problem is to use the fact that the sum of coefficients
of any polynomial p(x) =  is the value is the value
of this polynomial p(1) at x = 1, which is quite OBVIOUS.
Based on this idea, the sum of the coefficients in the quadratic function g(x) is g(1).
We don't know this value g(1), but from the problem we can calculate the composition f(g(1))
by substituting x= 1 into the given formula for f(g(x). We have then
f(g(1)) =  + +  + +  = =  = =  = =  = 27 2/9.
Now we can state that the value g(1), which we are looking for, is one of two possible roots of the equation
f(x) = 27 2/9,
or one of the two possible roots of the equation
5x^2 - 3x + 7 = 27 2/9.
In standard quadratic form, this equation is
5x^2 - 3x - 20 = 27 2/9.
Now we can state that the value g(1), which we are looking for, is one of two possible roots of the equation
f(x) = 27 2/9,
or one of the two possible roots of the equation
5x^2 - 3x + 7 = 27 2/9.
In standard quadratic form, this equation is
5x^2 - 3x - 20  = 0,
or, multiplying all the terms by 9, for convenience,
45x^2 - 27x - 182 = 0.
To find the roots, use the quadratic formula.
The roots are = 0,
or, multiplying all the terms by 9, for convenience,
45x^2 - 27x - 182 = 0.
To find the roots, use the quadratic formula.
The roots are  = =  and and  = =  .
So we conclude that the sum of the coefficients in the quadratic function g(x) is EITHER .
So we conclude that the sum of the coefficients in the quadratic function g(x) is EITHER  = 2 = 2 OR OR  = -1 = -1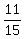 . ANSWER . ANSWER
Solved.
It is a nice Math circle level problem.
|
|
|
| |