SOLUTION: Determine whether f and g are inverse functions by evaluating f(g(x)) and g(f(x)). f(x)=x^2-2, domain [0, ∞) g(x)= {{{ sqrt( x+ 2 ) }}} , domain [-2,∞) Evaluate f(g(x)).

Question 1148429: Determine whether f and g are inverse functions by evaluating f(g(x)) and g(f(x)).
f(x)=x^2-2, domain [0, ∞)
g(x)= , domain [-2,∞)
Evaluate f(g(x)).
f(g(x))= (Simplify your answer.)
Evaluate g(f(x)).
g(f(x))= (Simplify your answer.)
Are f(x) and g(x) inverse functions?
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
these look like inverses of each other because f(g(x)) = x and g(f(x)) = x.

here's a reference.

http://home.windstream.net/okrebs/page45.html

you have f(x) = x^2-2.
the domain is [0,infinity)
the range is [-2,infinity)

you have g(x) = sqrt(x+2)
the domain is [-2,infinity)
the range is [0,infinity)

here's the graph of f(x) = x^2-2

$$$

here's the graph of g(x) = sqrt(x+2)

$$$

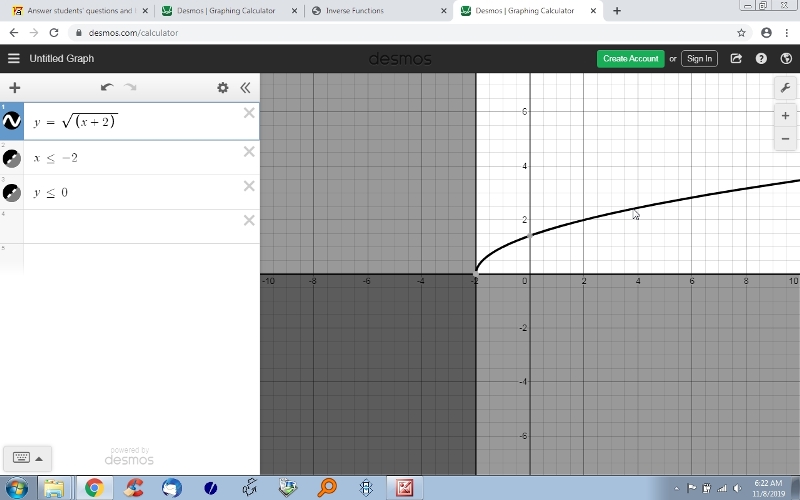
you solve for f(g(x)) as follows:

f(x) = x^2-2
g(x) = sqrt(x+2)
to get f(g(x)), you replace the x in f(x) with g(x).
this means you relace the x in f(x) with sqrt(x+2).
f(g(x)) = (sqrt(x+2))^2-2 = x+2-2 = x

g(x) = sqrt(x+2)
f(x) = x^2-2
to get g(f(x)), you replace the x in g(x) with f(x).
this means you replace the x in g(x) with x^2-2.
g(f(x)) = sqrt(x^2-2+2) = sqrt(x^2) = x

since f(g(x)) = x and g(f(x)) = x, then the two functions are inverse functions to each other.

RELATED QUESTIONS
3. If f(x)=square root 2x^2-1 and g(x)=x^1/2, find (and simplify) a) (f+g)(x) b)... (answered by CPhill)

If f(x)= square root 2x^2-1 and g(x)=x^1/2, find and simplify a) (f+g)(x) b) (f-g)(x) (answered by Alan3354)

verify that f and g are inverse functions f(x)=x+2... (answered by josgarithmetic)

If f(x) and g(x) are inverse functions what would... (answered by jim_thompson5910)

For each pair of functions f and g below, find f(g(x)) and g(f(x)). Then, determine... (answered by stanbon)

inverse functions: find f(g(x)) and g(f(x)) and determine whether the pair of functions... (answered by Edwin McCravy)

Consider the function f(x)=3x-6 and g(x)=x/3+2. A) Find f(g(x)). B) Find g(f(x)). C)... (answered by ReadingBoosters)

Determine whether the functions f(x) = 6x and g(x) = x/6 are inverse functions. (answered by jim_thompson5910)

functions f and g are defined as follows: f(x)=x^5 and g(x()= 1/x+1 Evaluate... (answered by Theo)