SOLUTION: Lady Lee needs TZS 57,500,000 at the end of the year 2029, and her only investment outlet is a 9 percent long term certificate of deposit from Puzzo Bank (compounded biannually). W

Question 1205437: Lady Lee needs TZS 57,500,000 at the end of the year 2029, and her only investment outlet is a 9 percent long term certificate of deposit from Puzzo Bank (compounded biannually). With the cectificate of deposit, she makes an initial investment at the beginning of the year 2023.
1:What single payment could be made at the beginning of the year 2023 to achieve thi objective?
W:What amount could Lady Lee invest at the end of each year annually up to the ye 2029 to achieve this same objective?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): You can put this solution on YOUR website!
she needs 57,500,000 at the end of 2029.
the initial investment is at the beginning of the year 2023.
the interest rate is 9% compounded semi-annually.

the semi-annual interest rate is 9% divided by 2 = 4.5% every 6 months.

2029 minus 2023 = 6 years.

you can use the calculator at https://arachnoid.com/finance/ to solve these problems.

1: What single payment could be made at the beginning of the year 2023 to achieve this objective?

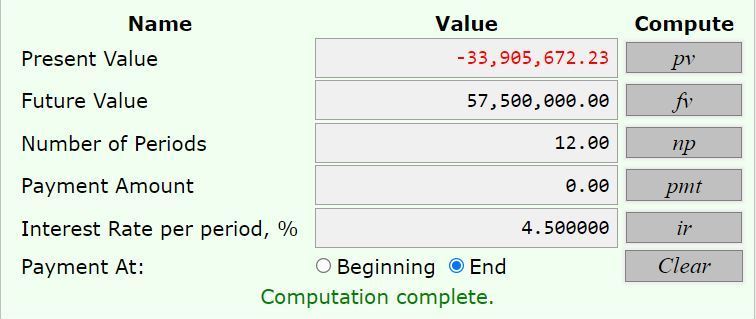
future value = 57,500,000
interest rate per semi-annual time period = 4.5%
number of time periods = 6 years * 2 semi-annual time periods per year = 12 semi-annual time periods.
payments per semi-annual time period = 0
payments made at the end of each semi-annual time period is not used.

calculator tells you that the present value needs to be 33,905,672.23.

here's what it looks like on the calculator.

2: What amount could Lady Lee invest at the end of each year annually up to the year 2029 to achieve this same objective?

use the same calculator.

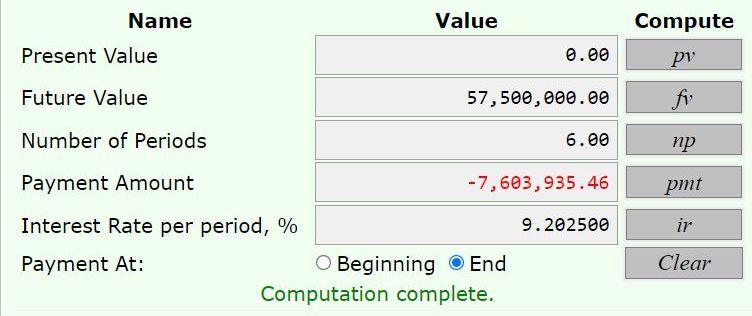
present value = 0
future value = 57,500,000
interest rate per annual time period = 9% per annual time period divided by 2 = 4.5% per semi-annual time period.
that is divided by 100 to get .045 and then has 1 added to it to get 1.045 and then raised to the power of 2 to get 1.045^2 = 1.092025 and then has 1 subtracted from it to get .092025 multiplied by 100 = 9.2025% per annual time period.
number of annual time periods = 6.
payments are made at the end of each annual time period.

calculator tells you that the payments made at the end of each annual time period = 7,603,935.46.

since the interest rate is compounded semi-annually, the nominal interest rate of 9.0 is divided by 2 to get a semi-annual interest rate of 4.5%.
that is then divided by 100 to get .045 and added to 1 to get 1.045 and raised to the power of 2 to get 1.045^2 = 1.092025.
it then has 1 subtracted from it to bet .092025 and is then multiplied by 100 to get 9.2025%.
that's the interest rate per annual time period used in the calculator for problem number 2.

here's what it looks like in the calculator.

le me know if you have any questions.

theo

Answer by ikleyn(52781)   (Show Source): You can put this solution on YOUR website!
.
Lady Lee needs TZS 57,500,000 at the end of the year 2029, and her only investment outlet
is a 9 percent long term certificate of deposit from Puzzo Bank (compounded biannually).
With the certificate of deposit, she makes an initial investment at the beginning of the year 2023.
(1) What single payment could be made at the beginning of the year 2023 to achieve this objective?
(2) What amount could Lady Lee invest at the end of each year annually up to the year 2029 to achieve this same objective?
~~~~~~~~~~~~~~~~~~~~~~~

        @Theo mistakenly determined that the deposit works 6 years.
        Actually, from the beginning of the year 2023 to the end of the year 2029,
        the deposit works and earns money 7 years (2029-2022 = 7 years).

        So, I came to bring a correct solution.

        I do not use an outside calculator, but make my calculations
        using explicit standard formulas of Financial Math with all necessary explanations.

Part 1. The formula for this 7 years deposit compounded semi-annually is FV = , where X is the unknown value of the initial deposit. From this formula, X = = 31,048,439.58. ANSWER to part 1. The value of the one-time initial deposit is TZS 31,048,439.58. Part 2. In this part 2, the situation is close to ordinary annuity account, but there is some difference. Since the account is replenished once per year, but is compounded twice per year semi-annually, we should and can use the scheme of the annually deposited and annually compounded ordinary annuity with the EFFECTIVE annual multiplicative growth rate of = 1.092025. So, we use the formula for the future value of the ordinary annuity FV = , where FV is the future value of the account; P is annual payment (deposit); r is the annual effective percentage rate presented as a decimal; n is the number of deposits (= the number of years, in this case). From this formula, you get for for the annual payment P = . (1) Under the given conditions, FV = 57,500,000; r = 0.092025; n = 7. So, according to the formula (1), you get for the annual payment P = = 6,211,008.91. Answer to part 2. The necessary annual deposit value is TZS 6,211,008.91 .

---------

On Ordinary Annuity saving plans, see the lessons
    - Ordinary Annuity saving plans and geometric progressions
    - Solved problems on Ordinary Annuity saving plans
in this site.

The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.

When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.

RELATED QUESTIONS
b) In a certain undertaking the initial investment is TZS 1,000,000,000. Expected... (answered by Theo)
(b) Show why the return on investment (ROI) and return on income (RI) may give... (answered by ikleyn)
Qn1. Revenue on consignment Sale: Dotto of Dodoma makes sewing machines at a cost of TZS... (answered by ikleyn)
A company wants to deposit $500,000 per year in an investment which earns an interest of... (answered by Theo)
A local university is planning to invest $500,000 every 3 months in an investment which... (answered by Theo)
a local university is planning to invest $ 500,000 every 3 months in an investment which... (answered by ikleyn)
If money is invested at r percent interest, compounded annually, the amount of the... (answered by Theo)
A finance company is offering an attractive rate of 15% per annum on investment and... (answered by solver91311)
A local university is planning to invest $500,000 every 3 months in an investment which... (answered by CPhill)