SOLUTION: Jane has a gas station that sells 90 Oct\ane gas and Low Sulphur Diesel. The station makes one order of fuel per week and she has enough space in her tanks for a total of 1150 gal

Question 1205182: Jane has a gas station that sells 90 Oct\ane gas and Low Sulphur Diesel. The station makes one
order of fuel per week and she has enough space in her tanks for a total of 1150 gallons of both
fuels. A gallon of 90 Octane gas cost US$0.75 and a gallon of Low Sulphur Diesel costs US$0.93
and they budget US$900 each week for repurchasing these products. The Manager estimates that
each week they will sell twice as much Diesel as 90 Octane gas. Profit per gallon of Low
Sulphur Diesel is US$4.15 and profit per gallon of 90 Octane is $3.60.
a. Formulate a Linear Programing model and determine the optimal mix of products that will
maximize profits. (9 marks)
b. Sketch the graph of the model you have developed. (5 marks)
c. What would be the effect on the optimal solution if the profit for Product B was moved from
$7 to $15. (6 marks)
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
x = gallons of 90 octane gas
y = gallons of low sulfur diesel
objective function is profit = 3.6x + 4.15y which you want to maximize
constraint inequalities are:
x + y <= 1150
.75x + .93y <= 900
y = 2x

using the desmox.com calculator, you would:
graph the opposite of the inequalities.
the area on the graph that is not shaded is the region of feasibility.
the maximum profit will be at the corner points of the feasible region.

here's the graph.

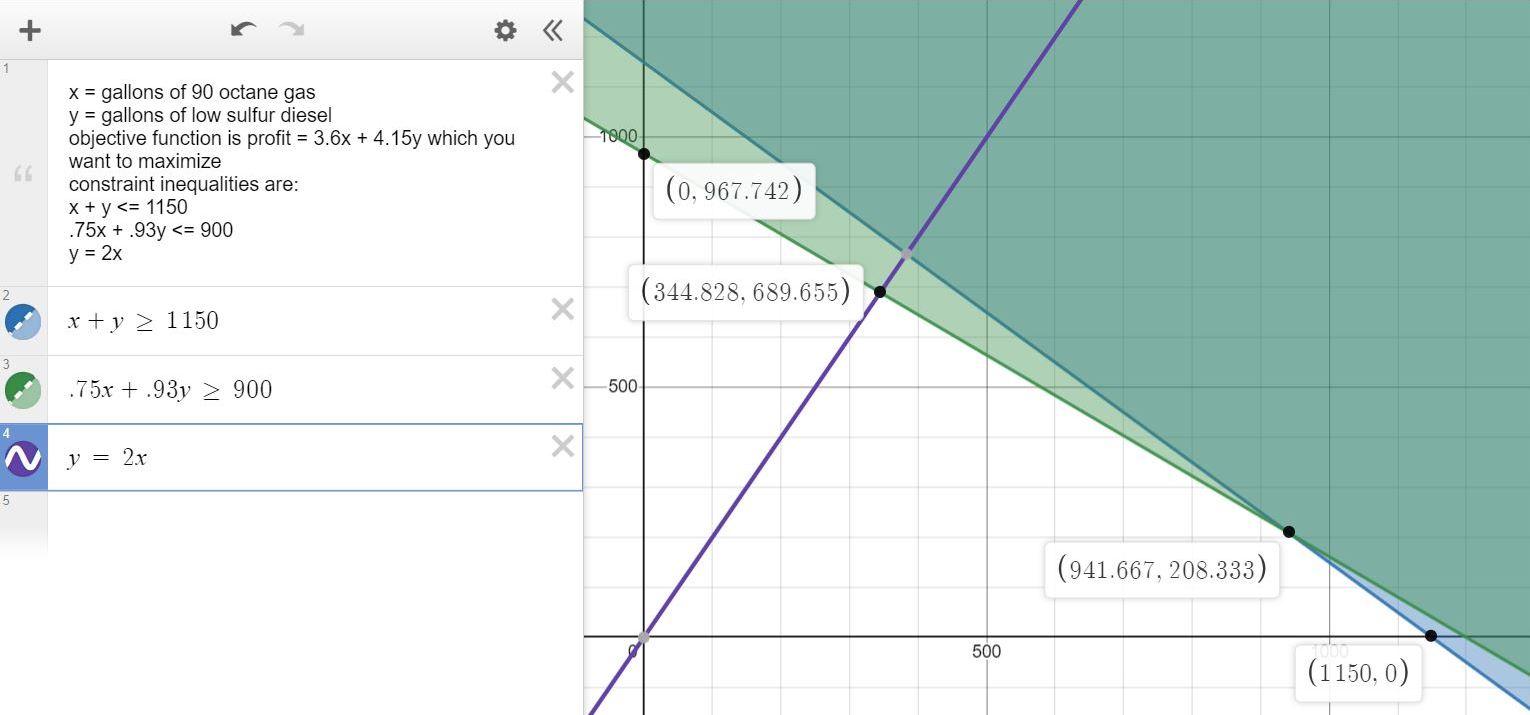
note that if you add the requirement that y = 2x, you force the solution to be on the line y = 2x.
the problem states that it is expected that they will sell twice as much diesel as 90 octane.
that is not a hard and fast requirement, but it is reasonable to assume that the maximum solution will be somewhere around that expectation.

without that requirement that y = 2x, your possible solutions are at the following corner points of the graph.
(0,967.742) = 0 * 3.6 + 967.742 * 4.15 = 4016.13
(344.828,689.655) = 344.828 * 3.6 + 689.655 * 4.15 = 4103.45
(941.667,208.333) = 941.667 * 3.6 + 208.333 * 4.15 = 4254.58 *****
(1150,0) = 1150 * 3.6 = 4140

maximum solution without the constraint that y = 2x is at (941.667,208.333) = 4254.58.
with that constraint, the solution is forced to be at (344,828,689.655) = 4103.45 which is the intersection of that line y = 2x with the line that borders the region of feasibility.

if you double the profit of diesel and leave everything else the same, then the maximum solution without the y = 2x constraint becomes 8032.26 at (0, 967.742).
with the constraint, the maximum solution remains at (344.828,689.655) with a total profit of 6965.62.
the same graph applies but the evaluation of the total profit changes.
the profit is not shown on the graph, but is evaluated with the new profit for diesel.
when the profit for diesel becomes 8.3, the profit equations become:
(0,967.742) = 0 * 3.6 + 967.742 * 8.3 = 8032.26 *****
(344.828,689.655) = 344.828 * 3.6 + 689.655 * 8.3 = 6965.52
(941.667,208.333) = 941.667 * 3.6 + 208.333 * 8.3 = 5119.18
(1150,0) = 1150 * 3.6 = 4140
without the y = 2x constraint, the new max profit is 8032.26 at (0,967.742)
with the y = 2x constraint, the new max profit is 6965.52 at (344.828,689.655).

RELATED QUESTIONS
A gas station sells a total of 4500 gallons of regular gas and premium gas in one day.... (answered by Boreal,MathTherapy)

A family has two cars. The first car has a fuel efficiency of miles per gallon of gas... (answered by Theo)

A family has two cars. The first car has a fuel efficiency of miles per gallon of gas... (answered by richwmiller)

A family has two cars. The first car has a fuel efficiency of miles per gallon of gas... (answered by ankor@dixie-net.com)

A family has two cars. The first car has a fuel efficiency of miles per gallon of gas and (answered by josgarithmetic)

A family has two cars. The first car has a fuel efficiency of miles per gallon of gas... (answered by josgarithmetic)

In one week, a gas station sells 1,250 gallons of gas. On average, how many quarts did... (answered by josgarithmetic)

A gas station owner makes a profit of 40 cents per gallon of gas he sells. How many... (answered by mananth)

A family has two cars. During one particular week, the first car consumed gallons of gas (answered by stanbon)