L2 equation is 3y + x - 20 = 0
convert both equations to slope intercept form as shown below:
for L1:
start with 2y - 3x - 6 = 0
add 6 to both sides to get 2y - 3x = 6
add 3x to both sides to get 2y = 3x + 6
divide both sides by 2 to get y = 3/2 * x + 3
that's the slope intercept form of the equation for L1.
for L2:
start with 3y + x - 20 = 0
add 20 to both sides to get 3y + x = 20
subtract x from both sides to get 3y = -x + 20
divide both sides by 3 to get y = -1/3 * x + 20/3
that's the slope intercept form of the equation for L2.
your two equations are:
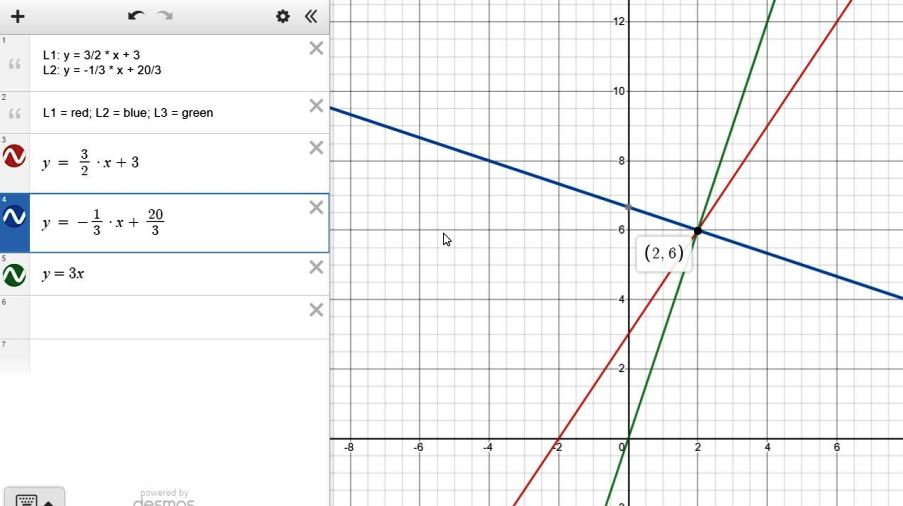
L1: y = 3/2 * x + 3
L2: y = -1/3 * x + 20/3
solve these two equations simultaneously as shown below:
subtract the second equation from the first to get:
0 = 3/2 * x + 1/3 * x + 3 - 20/3
multiply both sides of the equation by 6 to get:
0 = 9 * x + 2 * x + 18 - 40
combine like terms to get:
0 = 9 * x + 2 * x - 22
combine like terms to get:
0 = 11 * x - 22
add 22 to both sides to get:
22 = 11 * x
solve for x to get x = 22/11 = 2
when x = 2, the first eqution of y = 3/2 * x + 3 becomes y = 3/2 * 2 + 3 which b becomes y = 3 + 3 which becomes y = 6.
the intersection point for L1 and L2 is at (2,6).
you now want to find L3 perpendicular to L2 and going theough that point.
the slope intercept form of the equation of L3 will be y = mx + b.
m is the slope and b is the y-intercept.
the slope will be the negative reciprocal of the slope of L2.
the slope of L2 is equal to -1/3.
the slope of L3 will be 3 because negative reciprocal of -1/3 is 3/1 = 3.
the equation of L3 becomes y = 3 * x + b
since it passes through the point (2,6), then replace x with 2 and y with 6 to get:
6 = 3 * 2 + b
simplify to get 6 = 6 + b
solve for b to get:
b = 0
the equation of L3 is y = 3x
it is perpendicular to L2 because its slopw is a negative reciprocal of -1/3 and it passes through the point (2,6) which is the intersection point of L1 and L2 and now, L3.
the graph looks like this.