.
Find the remainder modulo 36 of 44427^3456789
~~~~~~~~~~~~~~
Notice that the remainder of the number 44427 divided by 36 is 3: 44427 = 36*1234 + 3.
In other words, 44427 == 3 (mod 36).
Therefore, 44427 modulo 36 is 3, and any degree  modulo 36 is equal to the same degree of 3 modulo 36.
Now, 3^2 == 9 mod 36
3^3 == 3*9 mod 36 == 27 mod 36
3^4 == 3*(3^3) mod 36 == 3*27 mod 36 == 81 mod 36 == 9 mod 36.
3^5 == 3*(3^4) mod 36 == 3*9 mod 36 == 27 mod 36.
3^6 == 3*(3^5) mod 36 == 3*27 mod 36 == 81 mod 36 == 9 mod 36.
You see that the degrees
modulo 36 is equal to the same degree of 3 modulo 36.
Now, 3^2 == 9 mod 36
3^3 == 3*9 mod 36 == 27 mod 36
3^4 == 3*(3^3) mod 36 == 3*27 mod 36 == 81 mod 36 == 9 mod 36.
3^5 == 3*(3^4) mod 36 == 3*9 mod 36 == 27 mod 36.
3^6 == 3*(3^5) mod 36 == 3*27 mod 36 == 81 mod 36 == 9 mod 36.
You see that the degrees 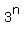 modulo 36 form a cyclic sequence
n 1 2 3 4 5 6 7 8 9
modulo 36 form a cyclic sequence
n 1 2 3 4 5 6 7 8 9
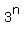 mod 36 3 9 27 9 27 9 27 9 27
Thus for n > 1,
mod 36 3 9 27 9 27 9 27 9 27
Thus for n > 1, 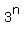 mod 36 is 9 for EVEN VALUES of n and is 27 for ODD VALUES of n.
It gives the ANSWER: 44427^3456789 modulo 36 is 27.
mod 36 is 9 for EVEN VALUES of n and is 27 for ODD VALUES of n.
It gives the ANSWER: 44427^3456789 modulo 36 is 27.
Solved.
------------------
A post-solution note
The fact that the remainders  modulo 36, or, wnich is the same, the remainders
modulo 36, or, wnich is the same, the remainders 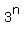 modulo 36 form
a periodic sequence seems to be a miracle.
+--------------------------------------------------------------------+
| But this fact is INEVITABLE consequence of simple properties. |
+--------------------------------------------------------------------+
If to consider the remainders modulo 36, there are only finite number of them:
0, 1, 2, . . . 10, 11, 12, . . . , 34, 35 --- in all, there are only 36 such remainders.
From the other side, the sequence 3, 3^2, 3^3, . . . , 3^k . . . is INFINITE.
Therefore, by projecting it into the sequence
modulo 36 form
a periodic sequence seems to be a miracle.
+--------------------------------------------------------------------+
| But this fact is INEVITABLE consequence of simple properties. |
+--------------------------------------------------------------------+
If to consider the remainders modulo 36, there are only finite number of them:
0, 1, 2, . . . 10, 11, 12, . . . , 34, 35 --- in all, there are only 36 such remainders.
From the other side, the sequence 3, 3^2, 3^3, . . . , 3^k . . . is INFINITE.
Therefore, by projecting it into the sequence 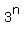 modulo 36, we INEVITABLY will have a repetition;
and as soon as such a repetition will happen for the first time, the periodic behavior and the period itself are just provided.
So, there is no any miracle in it - it is an inevitable fact.
The only heuristic is from which term does the period start and what is the length of the period?
These questions are easily to find out making an Excel spreadsheet - then it can be found out in seconds.
In the given problem, periods start from the second term and the length of the period is 2.
The facts I explained in this post-solution note, play a KEY ROLE in similar proofs, making a key for solving such problems.
Those who study Math from Math schools and/or from Math circles (or from associated Math books), usually know this remarkable property.
Now, after reading my post, you know this property, too (!)
So from now, you do belong to a category of those lucky persons who know everything about this miracle (!)
My congratulations (!) (!)
modulo 36, we INEVITABLY will have a repetition;
and as soon as such a repetition will happen for the first time, the periodic behavior and the period itself are just provided.
So, there is no any miracle in it - it is an inevitable fact.
The only heuristic is from which term does the period start and what is the length of the period?
These questions are easily to find out making an Excel spreadsheet - then it can be found out in seconds.
In the given problem, periods start from the second term and the length of the period is 2.
The facts I explained in this post-solution note, play a KEY ROLE in similar proofs, making a key for solving such problems.
Those who study Math from Math schools and/or from Math circles (or from associated Math books), usually know this remarkable property.
Now, after reading my post, you know this property, too (!)
So from now, you do belong to a category of those lucky persons who know everything about this miracle (!)
My congratulations (!) (!)