SOLUTION: Solve the following equations. 1. {x + 2y = 0 {x² + y² = 5 2. {x + y = 3 {x² + y² = 2

Regarding the first system of two equations,


express x = -2y  from the first equation and substitute to the second equation,
replacing x there.


You will get then


    (2y)^2 + y^2 = 5

     4y^2  + y^2 = 5

         5y^2    = 5

          y^2    = 1

          y  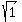    =  = +/- 1.


Thus you obtain two solutions:


    a)  for y = 1,   x = -2y = -2.


    b)  for y = -1,  x = -2y = 2.



ANSWER.  There are two solutions  (x,y) = (-2,1)  and  (x,y) = (2,-1).



These two solutions are two intersection points of the straight line  x + 2y = 0  and  the circle  x^2 + y^2 = 5.