SOLUTION: Find an equation for the circle that goes through the points (9,2) , (-1,12), and (-9,-4)
Algebra.Com
Question 1167474: Find an equation for the circle that goes through the points (9,2) , (-1,12), and (-9,-4)
Found 2 solutions by solver91311, Edwin McCravy:
Answer by solver91311(24713) (Show Source): You can put this solution on YOUR website!
Principle: You need to find the center of the circle and the measure of the radius. The perpendicular bisector of a chord of a circle passes through the center of the circle. The distance from the center of the circle to any one of the given points is the desired radius.
1. Choose one pair of given points and calculate the midpoint of that line segment.
2. Calculate the slope of the line containing the line segment.
3. Calculate the negative reciprocal of the slope calculated in step 1.
4. Using the Point-Slope form of an equation of a line with the midpoint from step 2 and the slope from step 3, derive an equation for the perpendicular bisector of the line segment defined by the points chosen in step 1.
)
5. Repeat steps 1 through 4 for a different pair of points.
6. Using the two equations from steps 4 and 5, solve the 2X2 system of linear equations to find the point of intersection of the two perpendicular bisectors of the two chosen chords. This will be the center of the circle.
7. Using the distance formula, calculate the distance from the center to any one of the given points:
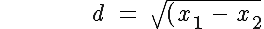^2\ +\ (y_1\,-\,y_2)^2})
Hint: Save yourself a little work. Since you will need the radius squared in the formulation of the equation of the circle, you need not actually take the square root in the distance formula.
8. The equation of a circle centered at ) with radius
with radius  is:
is:
^2\ +\ (y\,-\,k)^2\ =\ r^2)
.jpg)
John

My calculator said it, I believe it, that settles it

I > Ø

Answer by Edwin McCravy(20060) (Show Source): You can put this solution on YOUR website!
The other tutor did it using the method of construction of a circle through
three points. The center is the intersection of the perpendicular
bisector of two chords. It can be done that way. But when you have given
coordinates, the best way is to substitute the points in the general
equation for a circle:
Instead of doing your problem for you, I'll do a different one that is EXACTLY
like yours steop by step, that you can use as a guide for solving yours:
The one I'll solve is this one:
Find an equation for the circle that goes through the points (2,12) , (-7,3), and (11,3)
The general equation of the circle is:
Substituting (x,y) = (2,12)
Substituting (x,y) = (-7,3)
Substituting (x,y) = (11,3)
The system to solve is this:
Subtract the first two equations:
2A+12B+C=-148
-[-7A+ 3B+C= -58]
Change signs in bottom equation
2A+12B+C=-148
7A- 3B-C= 58
---------------
9A+ 9B = -90
Subtract the first and third equations:
2A+12B+C=-148
-[11A+ 3B+C=-130]
2A+12B+C=-148
-11A- 3B-C= 130
----------------
-9A+ 9B = -18
Subtract the second and third equations:
-7A+3B+C= -58
-[11A+3B+C=-130]
-7A+3B+C=-58
-11A-3B-C=130
---------------
-18A = 72
A = -4
Substituting back:
-9A+9B=-18
-9(-4)+9B =-18
36+9B =-18
9B =-54
B =-6
Substituting in
2A+12B+C=-148
2(-4)+12(-6)+C=-148
-8-72+C=-148
-80+C=-148
C=-68
So the equation of the circle
becomes
Now do yours the same way.
Edwin
RELATED QUESTIONS
Find an equation for the circle that goes through the these points (9,2) , (-1,12), and... (answered by Alan3354)
make an equation for the circle that goes through the points (9,2) , (-1,12), and... (answered by Edwin McCravy)
(-1 -9) and (2 0 )Find the equation of the line that goes through the... (answered by lynnlo)
Find an equation for the line that goes through the two intersection points of the circle
(answered by solver91311,ikleyn,MathTherapy)
9. Find the equation of the line that goes through the points (-4,1) and... (answered by jim_thompson5910)
Find the slope of the line that goes through the given points.
(3, -5), (-9, -8)... (answered by Alan3354)
Find the slope of the line that goes through the given points.
(3, -5), (-9, -8)... (answered by Alan3354)
Hi, these are five questions which I need help in
Write the general equation for the... (answered by Alan3354,Boreal,solver91311,ikleyn)
Find the equation of the line that passes through the points (9,-9) and... (answered by josgarithmetic)
.jpg)