the formula i used is f = p * (1 + r) ^ n
this formula will work off the difference between the temperature of the object and the temperature of the medium.
in the beginning, the difference is 700 - 200 = 500
after 3 minutes, the difference is 400 - 200 = 200
the formula becomes:
200 = 500 * (1 + r) ^ 3
solve for r to get:
r = (200/500) ^ (1/3) - 1
that gets you:
r = -.2631957003.
the formula becomes:
200 = 500 * (1 - .2631957003) ^ 3.
evaluate the equation to get:
200 = 200
this confirms the rate is correct.
after 6 minutes, the formula becomes:
f = 500 * (1 - .2631957003) ^ 6.
solve for f to get:
f = 80.
the difference is 80 after 6 minutes.
since the temperature of the medium is assumed to not change, that means the temperature of the object is 200 + 80 = 280 degrees.
note that, if the object was placed in the medium forever, then the assumption is that the object will becomes 200 degrees, same as the medium.
you can graph the function.
it looks like this.
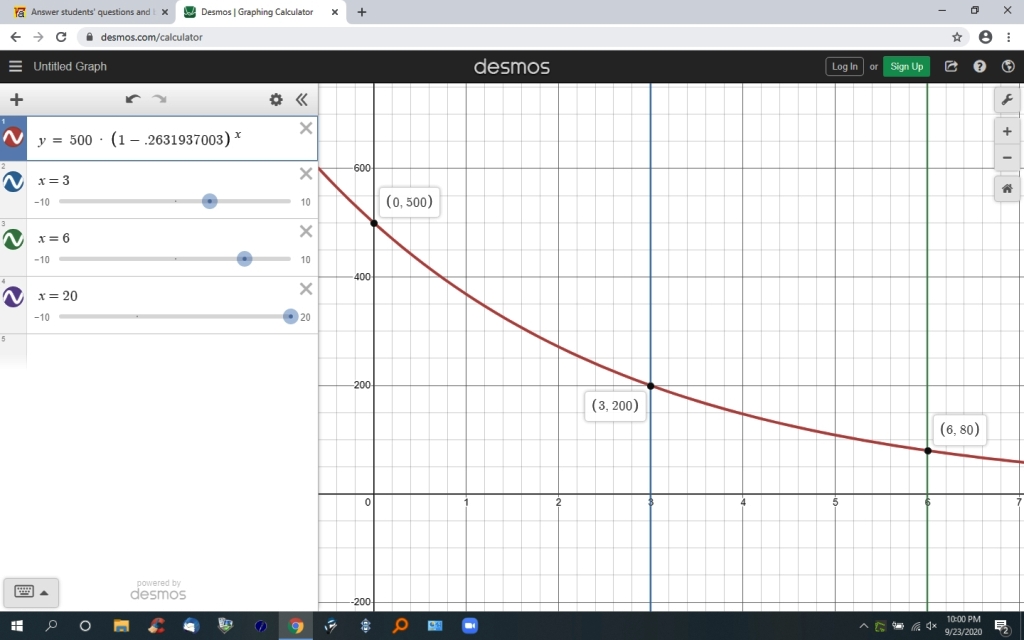
to test the claim that eventually it would become 200 degrees, make n a very large number and solve for that.
for example:
f = 500 * (1 - .2631937003) ^ 30 gets you:
f = .0524288.
the temperature of the object would then be 200.0524288 degrees.
that's pretty close to 200.
make n larger and it will get closer and closer to 200.
for example, when n = 60, f = .000005
round to anything less than 5 decimal digits and the difference is 0.