SOLUTION: The revenue function​ R(x) and the cost function​ C(x) for a particular product are given. These functions are valid only for the specified range of values. Find the nu
Algebra.Com
Question 1117851: The revenue function R(x) and the cost function C(x) for a particular product are given. These functions are valid only for the specified range of values. Find the number of units that must be produced to break even.
R(x)= 200x-x^2; C(x)=15x+6750
Answer by Theo(13342) (Show Source): You can put this solution on YOUR website!
R(x) = 200x - x^2
C(x) = 15x + 6750
to break even, R(x) = C(x).
that becomes:
200x - x^2 = 15x + 6750
subtract the right side of the equation from both sides of the equation to get:
200x - x^2 - 15x - 6750 = 0
combine like terms and re-arrange the terms in descending order of degree to get:
-x^2 + 185x - 6750 = 0
solve this quadratic equation to find the 0 points.
they will be at x = 50 or x = 135.
those are the number of units when you will break even.
between those 2 values, you will make money.
outside of those 2 values, you will lose money.
you should determine what the specified range of values are before answering, since not all of these may be in the specified range.
here's my graph of your equations showing the solution.
the first graph shows the intersection of the following 2 equations:
y = 200x - x^2 (your revenue equation)
y = 15x + 6750 (your cost equation).
the intersection of these 2 equations shows the break even point.
that's when the revenue equals the cost.
the second graph shows the result of setting the 2 equations equal to each other and then subtracting the right side of the equation from both sides of the equation.
that equation is y = -x^2 + 185x - 6750.
when y = 0, that's your break even point.
here are the two graphs.
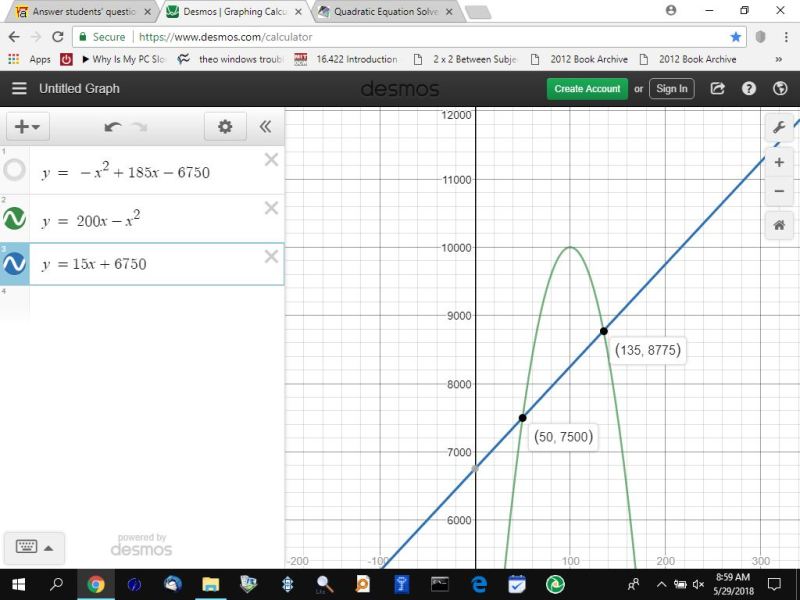
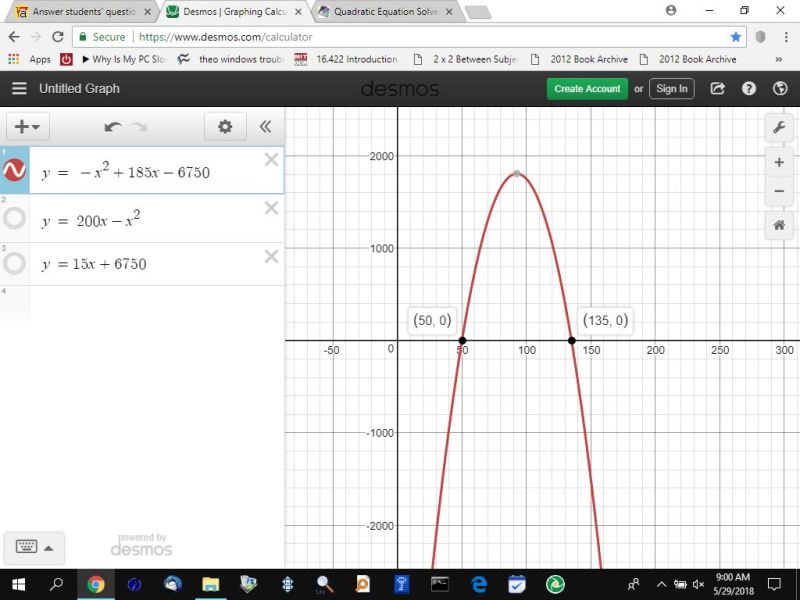
to find the revenue and the cost at the break even point, simply replace x with the indicated values of 50 or 135 and you will find that the revenue and the cost are equal to each other.
RELATED QUESTIONS
The revenue function R(x) and the cost function C(x) for a particular... (answered by Boreal)
The price p and the quantity x sold of a certain product obey the demand equation below.
(answered by Theo)
The price p and the quantity x sold of a certain product obey the demand equation below.
(answered by MathLover1)
Find the following for the function f(x)=lxl+20 ....note:the "l" next to x are... (answered by solver91311,Boreal)
Find the break-even point for the firm whose cost function C and revenue function R are... (answered by Fombitz)
The revenue function R(x) and the cost function C(x) for a particular product are... (answered by mananth)
The revenue function R(x) and the cost function C(x) for a particular product are... (answered by mananth)
The revenue function R(x) and the cost function C(x) for a particular product are... (answered by mananth)
find tehh break-even point for the firm whose cost function C and revenue function R are... (answered by ankor@dixie-net.com)

